


Next: Ion Acoustic Waves
Up: Waves in Warm Plasmas
Previous: Physics of Landau Damping
Plasma Dispersion Function
If the unperturbed distribution function, 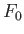 , appearing in Equation (8.23), is
a Maxwellian, then it is readily seen that, with a suitable scaling of the
variables, the dispersion relation for electrostatic
plasma waves can be expressed in terms of the
function
, appearing in Equation (8.23), is
a Maxwellian, then it is readily seen that, with a suitable scaling of the
variables, the dispersion relation for electrostatic
plasma waves can be expressed in terms of the
function
 |
(8.39) |
which is defined as it is written for
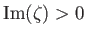 , and is
analytically continued for
, and is
analytically continued for
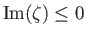 . This function is
known as the plasma dispersion function, and very often crops up
in problems involving small-amplitude waves propagating through
warm plasmas. Incidentally,
. This function is
known as the plasma dispersion function, and very often crops up
in problems involving small-amplitude waves propagating through
warm plasmas. Incidentally, 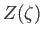 is the Hilbert transform of a Gaussian function.
is the Hilbert transform of a Gaussian function.
In view of the importance of the plasma dispersion function, and its regular
appearance in the literature of plasma physics, it is convenient to briefly examine its main
properties. We, first of all, note that if we differentiate 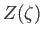 with
respect to
with
respect to  then we obtain
then we obtain
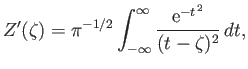 |
(8.40) |
which yields, on integration by parts,
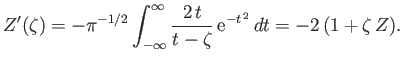 |
(8.41) |
If we let  tend to zero from the upper half of the complex plane, then we get
tend to zero from the upper half of the complex plane, then we get
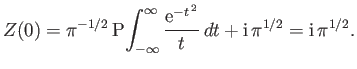 |
(8.42) |
Of course, the principal part integral is zero because its integrand is an
odd function of 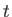 .
.
Integrating the linear differential equation (8.41), which possesses an
integrating factor
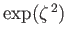 , and using the boundary condition
(8.42), we obtain an alternative expression for the plasma dispersion
function:
, and using the boundary condition
(8.42), we obtain an alternative expression for the plasma dispersion
function:
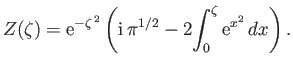 |
(8.43) |
Making the substitution
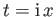 in the integral, and
noting that
in the integral, and
noting that
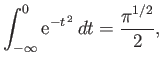 |
(8.44) |
we finally arrive at the expression
![$\displaystyle Z(\zeta) = 2\,{\rm i}\, {\rm e}^{-\zeta^{\,2}}\int_{-\infty}^{\,{...
... i}\,\pi^{1/2}\,{\rm e}^{-\zeta^{\,2}}\left[1+{\rm erf}({\rm i}\,\zeta)\right].$](img3123.png) |
(8.45) |
This formula, which relates the plasma dispersion function to an
error function of imaginary argument (Abramowitz and Stegun 1965b), is valid for all values
of  .
.
For small  , we have the expansion (Huba 2000c)
, we have the expansion (Huba 2000c)
![$\displaystyle Z(\zeta) = {\rm i}\,\pi^{1/2}\,{\rm e}^{-\zeta^{\,2}}-2\,\zeta\le...
...4\,\zeta^{\,4}}{15} - \frac{8\,\zeta^{\,6}}{105} +{\cal O}(\zeta^{\,8})\right].$](img3124.png) |
(8.46) |
For large  , where
, where
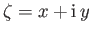 , the asymptotic expansion
for
, the asymptotic expansion
for 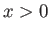 is written (Huba 2000c)
is written (Huba 2000c)
![$\displaystyle Z(\zeta) = {\rm i}\,\pi^{1/2}\,\sigma\,{\rm e}^{-\zeta^{\,2}} -\z...
...ac{3}{4\,\zeta^{\,4}}+\frac{15}{8\,\zeta^{\,6}} +{\cal O}(\zeta^{\,-8})\right].$](img3126.png) |
(8.47) |
Here,
![$\displaystyle \sigma = \left\{ \begin{array}{lll} 0&\mbox{\hspace{0.5cm}}& y>1/...
...vert y\vert<1/\vert x\vert\\ [0.5ex] 2&&y< -1/\vert x\vert \end{array} \right..$](img3127.png) |
(8.48) |
In deriving our previous expression (8.32) for the Landau damping rate, we, in effect, used the
first few terms of the asymptotic expansion (8.47).
The properties of the plasma dispersion function are specified in exhaustive
detail in a well-known book by Fried and Conte (Fried and Conte 1961).



Next: Ion Acoustic Waves
Up: Waves in Warm Plasmas
Previous: Physics of Landau Damping
Richard Fitzpatrick
2016-01-23


![]() with
respect to
with
respect to ![]() then we obtain
then we obtain
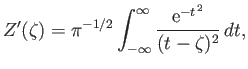
![]() tend to zero from the upper half of the complex plane, then we get
tend to zero from the upper half of the complex plane, then we get
![]() , and using the boundary condition
(8.42), we obtain an alternative expression for the plasma dispersion
function:
, and using the boundary condition
(8.42), we obtain an alternative expression for the plasma dispersion
function:
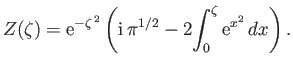
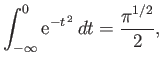
![$\displaystyle Z(\zeta) = 2\,{\rm i}\, {\rm e}^{-\zeta^{\,2}}\int_{-\infty}^{\,{...
... i}\,\pi^{1/2}\,{\rm e}^{-\zeta^{\,2}}\left[1+{\rm erf}({\rm i}\,\zeta)\right].$](img3123.png)
![]() , we have the expansion (Huba 2000c)
, we have the expansion (Huba 2000c)
![$\displaystyle Z(\zeta) = {\rm i}\,\pi^{1/2}\,{\rm e}^{-\zeta^{\,2}}-2\,\zeta\le...
...4\,\zeta^{\,4}}{15} - \frac{8\,\zeta^{\,6}}{105} +{\cal O}(\zeta^{\,8})\right].$](img3124.png)
![$\displaystyle \sigma = \left\{ \begin{array}{lll} 0&\mbox{\hspace{0.5cm}}& y>1/...
...vert y\vert<1/\vert x\vert\\ [0.5ex] 2&&y< -1/\vert x\vert \end{array} \right..$](img3127.png)