


Next: Waves in Magnetized Plasmas
Up: Waves in Warm Plasmas
Previous: Plasma Dispersion Function
Ion Acoustic Waves
If we now take ion dynamics into account then the dispersion relation (8.23),
for electrostatic plasma waves, generalizes to
 |
(8.49) |
that is, we simply add an extra term for the ions that has an
analogous form to the electron term. Let us search for a wave with
a phase-velocity, 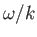 , that is much less than the electron thermal
velocity, but much greater than the ion thermal velocity. We may assume
that
, that is much less than the electron thermal
velocity, but much greater than the ion thermal velocity. We may assume
that
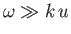 for the ion term, as we did previously for the
electron term. It follows that, to
lowest order, this term reduces to
for the ion term, as we did previously for the
electron term. It follows that, to
lowest order, this term reduces to
 , where
, where
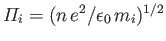 . Conversely, we
may assume that
. Conversely, we
may assume that
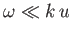 for the electron term. Thus, to
lowest order, we may neglect
for the electron term. Thus, to
lowest order, we may neglect 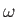 in the velocity space
integral. Assuming
in the velocity space
integral. Assuming 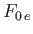 to be a Maxwellian with temperature
to be a Maxwellian with temperature 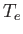 , the electron term reduces to
, the electron term reduces to
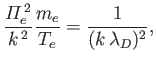 |
(8.50) |
where
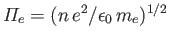 , and
, and
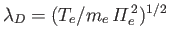 .
.
Thus, to a first approximation, the dispersion relation (8.49) can be written
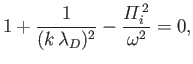 |
(8.51) |
giving
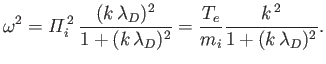 |
(8.52) |
For
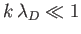 , we have
, we have
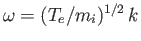 , a dispersion relation
which is like that of an ordinary sound wave, with the pressure provided by the
electrons, and the inertia by the ions. However, as the wavelength is reduced towards the
Debye length, the frequency levels off and approaches the ion plasma
frequency.
, a dispersion relation
which is like that of an ordinary sound wave, with the pressure provided by the
electrons, and the inertia by the ions. However, as the wavelength is reduced towards the
Debye length, the frequency levels off and approaches the ion plasma
frequency.
Let us check our original assumptions. In the long wavelength limit, we see that
the wave phase-velocity,
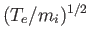 , is indeed much less than the
electron thermal velocity [by a factor
, is indeed much less than the
electron thermal velocity [by a factor
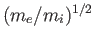 ], but that it
is only much greater than the ion thermal velocity if the ion temperature,
], but that it
is only much greater than the ion thermal velocity if the ion temperature,  ,
is much less than the electron temperature,
,
is much less than the electron temperature, 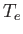 . In fact, if
. In fact, if
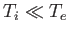 then the wave phase-velocity can simultaneously lie on almost flat portions of the
ion and electron distribution functions, as shown in Figure 8.7, implying that
the wave is subject to
very little Landau damping. Indeed,
then the wave phase-velocity can simultaneously lie on almost flat portions of the
ion and electron distribution functions, as shown in Figure 8.7, implying that
the wave is subject to
very little Landau damping. Indeed, 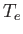 must generally be at least five to ten times greater than
must generally be at least five to ten times greater than  before an ion acoustic wave can propagate a distance of a few wavelengths
without being strongly damped (Cairns 1985).
before an ion acoustic wave can propagate a distance of a few wavelengths
without being strongly damped (Cairns 1985).
Of course, it is possible to obtain the ion acoustic wave dispersion relation,
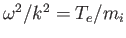 , using fluid theory. The kinetic theory used here
is an improvement on the fluid theory to the extent that no equation of
state is assumed, and also that the former theory makes it clear to us that ion acoustic waves are subject to
strong Landau damping (i.e., they cannot be considered normal modes of the
plasma) unless
, using fluid theory. The kinetic theory used here
is an improvement on the fluid theory to the extent that no equation of
state is assumed, and also that the former theory makes it clear to us that ion acoustic waves are subject to
strong Landau damping (i.e., they cannot be considered normal modes of the
plasma) unless
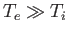 .
.
Figure:
Ion and electron distribution functions with
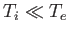 .
.
 |



Next: Waves in Magnetized Plasmas
Up: Waves in Warm Plasmas
Previous: Plasma Dispersion Function
Richard Fitzpatrick
2016-01-23

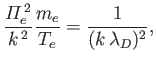
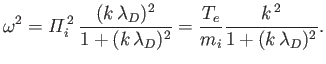
![]() , is indeed much less than the
electron thermal velocity [by a factor
, is indeed much less than the
electron thermal velocity [by a factor
![]() ], but that it
is only much greater than the ion thermal velocity if the ion temperature,
], but that it
is only much greater than the ion thermal velocity if the ion temperature, ![]() ,
is much less than the electron temperature,
,
is much less than the electron temperature, ![]() . In fact, if
. In fact, if
![]() then the wave phase-velocity can simultaneously lie on almost flat portions of the
ion and electron distribution functions, as shown in Figure 8.7, implying that
the wave is subject to
very little Landau damping. Indeed,
then the wave phase-velocity can simultaneously lie on almost flat portions of the
ion and electron distribution functions, as shown in Figure 8.7, implying that
the wave is subject to
very little Landau damping. Indeed, ![]() must generally be at least five to ten times greater than
must generally be at least five to ten times greater than ![]() before an ion acoustic wave can propagate a distance of a few wavelengths
without being strongly damped (Cairns 1985).
before an ion acoustic wave can propagate a distance of a few wavelengths
without being strongly damped (Cairns 1985).
![]() , using fluid theory. The kinetic theory used here
is an improvement on the fluid theory to the extent that no equation of
state is assumed, and also that the former theory makes it clear to us that ion acoustic waves are subject to
strong Landau damping (i.e., they cannot be considered normal modes of the
plasma) unless
, using fluid theory. The kinetic theory used here
is an improvement on the fluid theory to the extent that no equation of
state is assumed, and also that the former theory makes it clear to us that ion acoustic waves are subject to
strong Landau damping (i.e., they cannot be considered normal modes of the
plasma) unless
![]() .
.