


Next: Fresnel Relations
Up: Wave Propagation in Inhomogeneous
Previous: Introduction
Laws of Geometric Optics
Suppose that the region 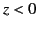 is occupied by a transparent dielectric medium of uniform refractive index
is occupied by a transparent dielectric medium of uniform refractive index 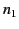 , whereas
the region
, whereas
the region 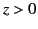 is occupied by a second transparent dielectric medium of uniform refractive index
is occupied by a second transparent dielectric medium of uniform refractive index  . (See Figure 14.) Let a plane light wave be launched toward positive
. (See Figure 14.) Let a plane light wave be launched toward positive  from a
light source of angular frequency
from a
light source of angular frequency  located at large negative
located at large negative  . Furthermore, suppose that this wave, which has the wavevector
. Furthermore, suppose that this wave, which has the wavevector 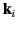 , is obliquely incident on the interface between the two media. We would expect the incident plane wave to be partially reflected and partially
refracted (i.e., transmitted) by the interface.
Let the reflected and refracted plane waves have the wavevectors
, is obliquely incident on the interface between the two media. We would expect the incident plane wave to be partially reflected and partially
refracted (i.e., transmitted) by the interface.
Let the reflected and refracted plane waves have the wavevectors
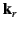 and
and 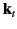 , respectively. (See Figure 14.) Hence, we can write
, respectively. (See Figure 14.) Hence, we can write
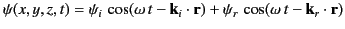 |
(946) |
in the region 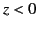 , and
, and
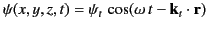 |
(947) |
in the region 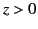 . Here,
. Here,
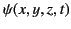 represents the magnetic component of the resultant light wave,
represents the magnetic component of the resultant light wave, 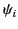 the
amplitude of the incident wave,
the
amplitude of the incident wave, 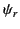 the amplitude of the reflected wave, and
the amplitude of the reflected wave, and 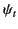 the amplitude of the
refracted wave. All of the component waves have the same angular frequency,
the amplitude of the
refracted wave. All of the component waves have the same angular frequency,  , because this property is
ultimately determined by the wave source. Furthermore, if the magnetic component of an electromagnetic wave is specified then the electric
component of the wave is fully determined, and vice versa. (See Section 7.1.)
, because this property is
ultimately determined by the wave source. Furthermore, if the magnetic component of an electromagnetic wave is specified then the electric
component of the wave is fully determined, and vice versa. (See Section 7.1.)
In general, the wavefunction,  , must be continuous at
, must be continuous at 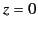 , because there cannot be a discontinuity in either the
normal or the tangential component of a magnetic field across an interface between two (non-magnetic) dielectric media. (The same is not true of an electric field, which can have a normal discontinuity across
an interface between two dielectric media.) This explains why we have chosen
, because there cannot be a discontinuity in either the
normal or the tangential component of a magnetic field across an interface between two (non-magnetic) dielectric media. (The same is not true of an electric field, which can have a normal discontinuity across
an interface between two dielectric media.) This explains why we have chosen  to represent the magnetic, rather than the electric,
component of the wave. Thus, the matching condition at
to represent the magnetic, rather than the electric,
component of the wave. Thus, the matching condition at 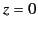 takes the form
takes the form
![$\displaystyle \psi_i\,\cos(\omega\,t-k_{i\,x}\,x-k_{i\,y}\,y)\\ [0.5ex] + \psi_...
...ga\,t-k_{r\,x}\,x-k_{r\,y}\,y)=\psi_t\,\cos(\omega\,t-k_{t\,x}\,x-k_{t\,y}\,y).$](img2024.png) |
(948) |
This condition must be satisfied at all values of  ,
, 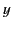 , and
, and 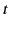 . This is only possible if
. This is only possible if
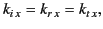 |
(949) |
and
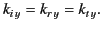 |
(950) |
Suppose that the direction of propagation of the incident wave lies in the  -
- plane, so that
plane, so that
 . It immediately
follows, from Equation (951), that
. It immediately
follows, from Equation (951), that
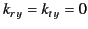 . In other words, the directions of propagation of the reflected
and the refracted waves also lie in the
. In other words, the directions of propagation of the reflected
and the refracted waves also lie in the  -
- plane, which implies that
plane, which implies that 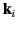 ,
, 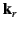 and
and 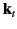 are
co-planar vectors. This constraint is implicit in the well-known laws of
geometric optics.
are
co-planar vectors. This constraint is implicit in the well-known laws of
geometric optics.
Figure 14:
Reflection and refraction of a plane wave at a plane boundary.
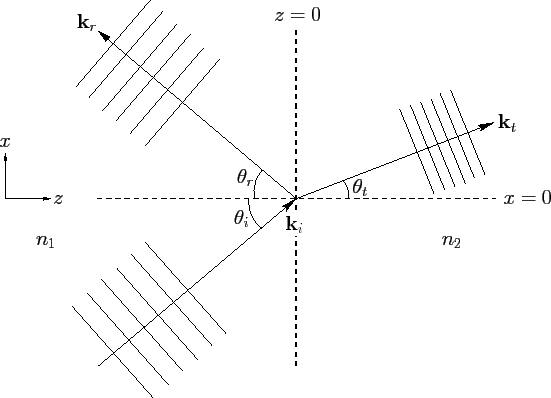 |
Assuming that the previously mentioned constraint is satisfied, let the incident, reflected, and refracted wave normals subtend
angles 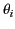 ,
, 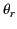 , and
, and 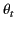 with the
with the  -axis, respectively. (See Figure 14.) It follows that
-axis, respectively. (See Figure 14.) It follows that
where
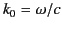 is the vacuum wavenumber, and
is the vacuum wavenumber, and 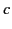 the velocity of light in vacuum.
Here, we have made use of the fact that wavenumber (i.e., the magnitude of the wavevector) of a light wave propagating through a dielectric medium of
refractive index
the velocity of light in vacuum.
Here, we have made use of the fact that wavenumber (i.e., the magnitude of the wavevector) of a light wave propagating through a dielectric medium of
refractive index 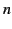 is
is 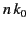 .
.
According to Equation (950),
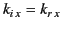 , which yields
, which yields
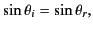 |
(954) |
and
 , which reduces to
, which reduces to
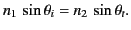 |
(955) |
The first of these relations states that the angle of incidence, 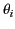 , is equal to the angle of reflection,
, is equal to the angle of reflection, 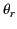 . This is the
familiar law of reflection. Furthermore, the second relation corresponds to the equally familiar
law of refraction, otherwise known as Snell's law.
. This is the
familiar law of reflection. Furthermore, the second relation corresponds to the equally familiar
law of refraction, otherwise known as Snell's law.
Incidentally, the fact that a plane wave propagates through a uniform
dielectric medium with a constant wavevector, and, therefore, a constant direction of motion, is equivalent to the well-known law of rectilinear propagation, which
states that a light ray (i.e., the normal to a constant phase surface) propagates through a uniform medium in a straight-line.
It follows, from the previous discussion, that the laws of geometric optics (i.e., the law
of rectilinear propagation, the law of reflection, and the law of refraction) are fully consistent with the
wave properties of light, despite the fact that they do not seem to explicitly depend on these properties.



Next: Fresnel Relations
Up: Wave Propagation in Inhomogeneous
Previous: Introduction
Richard Fitzpatrick
2014-06-27
![]() , must be continuous at
, must be continuous at ![]() , because there cannot be a discontinuity in either the
normal or the tangential component of a magnetic field across an interface between two (non-magnetic) dielectric media. (The same is not true of an electric field, which can have a normal discontinuity across
an interface between two dielectric media.) This explains why we have chosen
, because there cannot be a discontinuity in either the
normal or the tangential component of a magnetic field across an interface between two (non-magnetic) dielectric media. (The same is not true of an electric field, which can have a normal discontinuity across
an interface between two dielectric media.) This explains why we have chosen ![]() to represent the magnetic, rather than the electric,
component of the wave. Thus, the matching condition at
to represent the magnetic, rather than the electric,
component of the wave. Thus, the matching condition at ![]() takes the form
takes the form
![]() -
-![]() plane, so that
plane, so that
![]() . It immediately
follows, from Equation (951), that
. It immediately
follows, from Equation (951), that
![]() . In other words, the directions of propagation of the reflected
and the refracted waves also lie in the
. In other words, the directions of propagation of the reflected
and the refracted waves also lie in the ![]() -
-![]() plane, which implies that
plane, which implies that ![]() ,
, ![]() and
and ![]() are
co-planar vectors. This constraint is implicit in the well-known laws of
geometric optics.
are
co-planar vectors. This constraint is implicit in the well-known laws of
geometric optics.
![]() ,
, ![]() , and
, and ![]() with the
with the ![]() -axis, respectively. (See Figure 14.) It follows that
-axis, respectively. (See Figure 14.) It follows that
![]() , which yields
, which yields