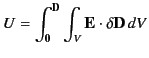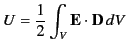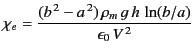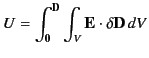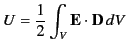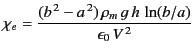Next: Magnetostatic Fields
Up: Electrostatics in Dielectric Media
Previous: Dielectric Liquids in Electrostatic
- Starting from Equation (201), derive the result
 .
.
- Consider an electron of charge
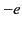 moving in a circular orbit of radius
moving in a circular orbit of radius 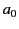 about a charge
about a charge 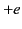 in a field directed at right angles to the
plane of the orbit. Show that the polarizability
in a field directed at right angles to the
plane of the orbit. Show that the polarizability 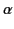 is approximately
is approximately
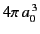 .
.
- A point charge
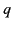 is located in free space a distance
is located in free space a distance 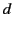 from the center of a dielectric sphere of radius
from the center of a dielectric sphere of radius  (
(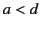 ) and
dielectric constant
) and
dielectric constant  . Find the potential at all points in space as an expansion in spherical harmonics. Calculate
the rectangular components of the electric field in the vicinity of the center of the sphere.
. Find the potential at all points in space as an expansion in spherical harmonics. Calculate
the rectangular components of the electric field in the vicinity of the center of the sphere.
- A dielectric sphere of radius
 and dielectric constant
and dielectric constant
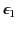 is imbedded in an infinite dielectric block of
dielectric constant
is imbedded in an infinite dielectric block of
dielectric constant
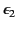 . The block is placed in a uniform electric field
. The block is placed in a uniform electric field
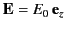 . In other words, if
. In other words, if
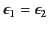 then the electric field would be
then the electric field would be
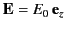 . Find the potential both inside
and outside the sphere (assuming that
. Find the potential both inside
and outside the sphere (assuming that
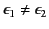 ), and the distribution of bound charges on the surface of the sphere.
), and the distribution of bound charges on the surface of the sphere.
- An electric dipole of moment
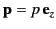 lies at the center of a spherical cavity of radius
lies at the center of a spherical cavity of radius  in a uniform dielectric material of relative dielectric constant
in a uniform dielectric material of relative dielectric constant  . Find the electrostatic potential
throughout space. Find the bound charge sheet density on the surface of the
cavity.
. Find the electrostatic potential
throughout space. Find the bound charge sheet density on the surface of the
cavity.
- A cylindrical coaxial cable consists of a thin inner conductor of radius
 ,
surrounded by a dielectric sheath of dielectric constant
,
surrounded by a dielectric sheath of dielectric constant
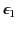 and outer radius
and outer radius  , surrounded by a second dielectric sheath of
dielectric constant
, surrounded by a second dielectric sheath of
dielectric constant
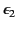 and outer radius
and outer radius 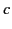 , surrounded
by a thin outer conductor. All components of the cable are touching. What
is the capacitance per unit length of the cable?
, surrounded
by a thin outer conductor. All components of the cable are touching. What
is the capacitance per unit length of the cable?
- A very long, right circular, cylindrical shell of dielectric constant
 and inner and outer radii
and inner and outer radii  and
and  , respectively,
is placed in a previously uniform electric field
, respectively,
is placed in a previously uniform electric field 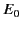 with its axis perpendicular to the field. The medium inside and outside the
cylinder has a dielectric constant of unity. Determine the potential in the three regions, neglecting end effects.
Discuss the limiting forms of your solutions for a solid dielectric cylinder in a uniform field, and a cylindrical cavity in a
uniform dielectric.
with its axis perpendicular to the field. The medium inside and outside the
cylinder has a dielectric constant of unity. Determine the potential in the three regions, neglecting end effects.
Discuss the limiting forms of your solutions for a solid dielectric cylinder in a uniform field, and a cylindrical cavity in a
uniform dielectric.
- Suppose that
where the dielectric tensor,
 , is constant (i.e., it is indepedent of
, is constant (i.e., it is indepedent of 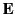 ).
Demonstrate that
).
Demonstrate that
can only be integrated to give
if
 is symmetric. (Incidentally, because we generally expect a dielectric system to be conservative, this proves that
is symmetric. (Incidentally, because we generally expect a dielectric system to be conservative, this proves that
 must be a
symmetric tensor, otherwise the final energy of a dielectric system would not be independent of its past history.)
must be a
symmetric tensor, otherwise the final energy of a dielectric system would not be independent of its past history.)
- Show that for an electret (i.e., a material of fixed
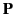 ) the integral
) the integral
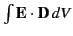 over all space vanishes.
over all space vanishes.
- Two long, coaxial, cylindrical conducting surfaces of radii
 and
and  (
(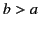 ) are lowered vertically into a
liquid dielectric. If the liquid rises a mean height
) are lowered vertically into a
liquid dielectric. If the liquid rises a mean height 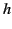 between the electrodes when a potential difference
between the electrodes when a potential difference  is
established between them, show that the susceptibility of the liquid is
is
established between them, show that the susceptibility of the liquid is
where 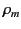 is the mass density of the liquid,
is the mass density of the liquid, 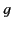 the acceleration due to gravity, and the susceptibility of air is neglected.
the acceleration due to gravity, and the susceptibility of air is neglected.



Next: Magnetostatic Fields
Up: Electrostatics in Dielectric Media
Previous: Dielectric Liquids in Electrostatic
Richard Fitzpatrick
2014-06-27