


Next: Scalar and Vector Potentials
Up: Maxwell's Equations
Previous: Introduction
Maxwell's Equations
All classical (i.e., non-quantum) electromagnetic phenomena are governed by Maxwell's equations, which
take the form
Here,
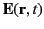 ,
,
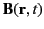 ,
,
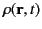 , and
, and
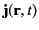 represent the electric field-strength, the
magnetic field-strength, the electric charge density, and the electric current density, respectively.
Moreover,
represent the electric field-strength, the
magnetic field-strength, the electric charge density, and the electric current density, respectively.
Moreover,
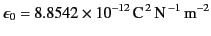 |
(5) |
is the electric permittivity of free space, whereas
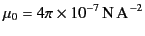 |
(6) |
is the magnetic permeability of free space. As is well known, Equation (1) is equivalent to Coulomb's law (for the electric fields generated by point charges), Equation (2)
is equivalent to the statement that magnetic monopoles do not exist (which implies that magnetic field-lines can never begin or end),
Equation (3) is equivalent to Faraday's law of electromagnetic induction, and Equation (4) is equivalent to the Biot-Savart law
(for the magnetic fields generated by line currents) augmented by the induction of magnetic fields by changing electric fields.
Maxwell's equations are linear in nature. In other words, if
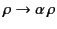 and
and
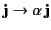 , where
, where 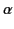 is
an arbitrary (spatial and temporal) constant, then it is clear from Equations (1)-(4) that
is
an arbitrary (spatial and temporal) constant, then it is clear from Equations (1)-(4) that
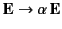 and
and
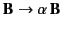 . The linearity of Maxwell's equations accounts for the well-known fact that the electric fields generated by point charges, as well as the magnetic
fields generated by line currents, are superposable.
. The linearity of Maxwell's equations accounts for the well-known fact that the electric fields generated by point charges, as well as the magnetic
fields generated by line currents, are superposable.
Taking the divergence of Equation (4), and combining the resulting expression with Equation (1), we obtain
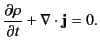 |
(7) |
In integral form, making use of the divergence theorem, this equation becomes
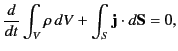 |
(8) |
where 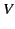 is a fixed volume bounded by a surface
is a fixed volume bounded by a surface 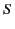 . The volume integral represents the net electric charge contained within the volume,
whereas the surface integral represents the outward flux of charge across the bounding surface. The previous equation, which states that the net rate of change of the charge contained within the volume
. The volume integral represents the net electric charge contained within the volume,
whereas the surface integral represents the outward flux of charge across the bounding surface. The previous equation, which states that the net rate of change of the charge contained within the volume 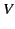 is
equal to minus the net flux of charge across the bounding surface
is
equal to minus the net flux of charge across the bounding surface 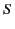 , is
clearly a statement of the conservation of electric charge. Thus, Equation (7) is the differential form of this conservation equation.
, is
clearly a statement of the conservation of electric charge. Thus, Equation (7) is the differential form of this conservation equation.
As is well known, a point electric charge 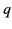 moving with velocity
moving with velocity 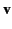 in the presence of an electric field
in the presence of an electric field 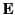 and a magnetic field
and a magnetic field 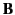 experiences a force
experiences a force
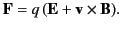 |
(9) |
Likewise, a distributed charge distribution of charge density 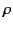 and current density
and current density 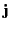 experiences a force density
experiences a force density
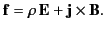 |
(10) |



Next: Scalar and Vector Potentials
Up: Maxwell's Equations
Previous: Introduction
Richard Fitzpatrick
2014-06-27
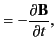
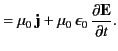
![]() and
and
![]() , where
, where ![]() is
an arbitrary (spatial and temporal) constant, then it is clear from Equations (1)-(4) that
is
an arbitrary (spatial and temporal) constant, then it is clear from Equations (1)-(4) that
![]() and
and
![]() . The linearity of Maxwell's equations accounts for the well-known fact that the electric fields generated by point charges, as well as the magnetic
fields generated by line currents, are superposable.
. The linearity of Maxwell's equations accounts for the well-known fact that the electric fields generated by point charges, as well as the magnetic
fields generated by line currents, are superposable.
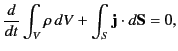
![]() moving with velocity
moving with velocity ![]() in the presence of an electric field
in the presence of an electric field ![]() and a magnetic field
and a magnetic field ![]() experiences a force
experiences a force