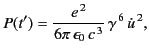Next: Synchrotron Radiation
Up: Relativity and Electromagnetism
Previous: Radiation Losses
In order to calculate the angular distribution of the energy radiated by an
accelerated charge, we must think carefully about what is meant by the
rate of radiation of the charge. This quantity is
actually the amount of
energy lost by the charge in a retarded time interval  during the
emission of the signal. Thus,
during the
emission of the signal. Thus,
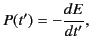 |
(1952) |
where 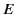 is the energy of the charge. The Poynting vector
is the energy of the charge. The Poynting vector
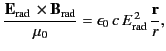 |
(1953) |
where use has been made of
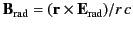 [see Equation (1916)],
represents the energy flux per unit actual time,
[see Equation (1916)],
represents the energy flux per unit actual time,  .
Thus, the energy loss rate
of the charge into a given element of solid angle
.
Thus, the energy loss rate
of the charge into a given element of solid angle
 is
is
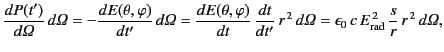 |
(1954) |
where use has been made of Equation (1902). Here,  and
and 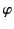 are angular coordinates used to locate the element of solid angle.
It follows from Equation (1922) that
are angular coordinates used to locate the element of solid angle.
It follows from Equation (1922) that
![$\displaystyle \frac{dP(t')}{d{\mit\Omega}} = \frac{e^{\,2}\, r}{16\pi^2\, \epsilon_0\, c^{\,3}} \frac{[{\bf r}\times({\bf r}_u\times\dot{\bf u})]^2}{s^{\,5}}.$](img4097.png) |
(1955) |
Consider the special case in which the direction of acceleration
coincides with the direction of motion. Let us define spherical polar
coordinates whose axis points along this common direction. It is
easily demonstrated that, in this case, the previous expression reduces to
![$\displaystyle \frac{d P(t')}{d{\mit\Omega}} = \frac{e^{\,2}\,\dot{u}^{\,2}}{16\pi^2\, \epsilon_0\, c^{\,3}} \frac{\sin^2\theta}{[1-(u/c)\,\cos\theta]^5}.$](img4098.png) |
(1956) |
In the non-relativistic limit,
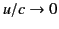 , the radiation
pattern has the familiar
, the radiation
pattern has the familiar
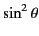 dependence of dipole radiation. In
particular, the pattern is symmetric in the forward (
dependence of dipole radiation. In
particular, the pattern is symmetric in the forward (
 )
and backward (
)
and backward (
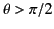 ) directions. However, as
) directions. However, as
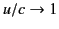 ,
the radiation pattern becomes more and more concentrated in the forward
direction. The angle
,
the radiation pattern becomes more and more concentrated in the forward
direction. The angle
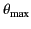 for which the intensity
is a maximum is
for which the intensity
is a maximum is
![$\displaystyle \theta_{\rm max} = \cos^{-1} \left[ \frac{1}{3\, u/c}\left(\sqrt{1+ 15 \,u^{\,2}/c^{\,2}} - 1\right)\right].$](img4103.png) |
(1957) |
This expression yields
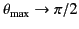 as
as
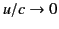 , and
, and
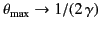 as
as
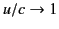 . Thus, for a highly relativistic charge, the
radiation is emitted in a narrow cone whose axis is aligned
along the direction of motion.
In this case, the angular distribution (1958) reduces to
. Thus, for a highly relativistic charge, the
radiation is emitted in a narrow cone whose axis is aligned
along the direction of motion.
In this case, the angular distribution (1958) reduces to
![$\displaystyle \frac{dP(t')}{d{\mit\Omega}} \simeq \frac{2\, e^{\,2}\,\dot{u}^{\...
...,\gamma^{\,8} \frac{(\gamma\,\theta)^{\,2}}{[1+ (\gamma\,\theta)^{\,2}]^{\,5}}.$](img4106.png) |
(1958) |
The total power radiated by the charge is obtained by integrating Equation (1958)
over all solid angles. We obtain
![$\displaystyle P(t')= \frac{e^{\,2}\,\dot{u}^{\,2}}{8\pi \,\epsilon_0\, c^{\,3}}...
...n_0 \,c^{\,3}} \int_{-1}^{+1} \frac{(1-\mu^{\,2})\,d\mu}{[1-(u/c)\,\mu]^{\,5}}.$](img4107.png) |
(1959) |
It is easily verified that
![$\displaystyle \int_{-1}^{+1}\frac{(1-\mu^{\,2})\,d\mu}{[1-(u/c)\,\mu]^{\,5}} = \frac{4}{3}\,\gamma^{\,6}.$](img4108.png) |
(1960) |
Hence,
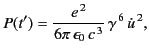 |
(1961) |
which agrees with Equation (1946), provided that
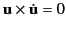 .
.



Next: Synchrotron Radiation
Up: Relativity and Electromagnetism
Previous: Radiation Losses
Richard Fitzpatrick
2014-06-27
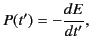
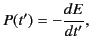
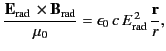
![$\displaystyle \frac{dP(t')}{d{\mit\Omega}} = \frac{e^{\,2}\, r}{16\pi^2\, \epsilon_0\, c^{\,3}} \frac{[{\bf r}\times({\bf r}_u\times\dot{\bf u})]^2}{s^{\,5}}.$](img4097.png)
![$\displaystyle \theta_{\rm max} = \cos^{-1} \left[ \frac{1}{3\, u/c}\left(\sqrt{1+ 15 \,u^{\,2}/c^{\,2}} - 1\right)\right].$](img4103.png)
![$\displaystyle P(t')= \frac{e^{\,2}\,\dot{u}^{\,2}}{8\pi \,\epsilon_0\, c^{\,3}}...
...n_0 \,c^{\,3}} \int_{-1}^{+1} \frac{(1-\mu^{\,2})\,d\mu}{[1-(u/c)\,\mu]^{\,5}}.$](img4107.png)
![$\displaystyle \int_{-1}^{+1}\frac{(1-\mu^{\,2})\,d\mu}{[1-(u/c)\,\mu]^{\,5}} = \frac{4}{3}\,\gamma^{\,6}.$](img4108.png)