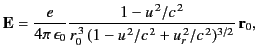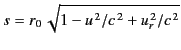Next: Larmor Formula
Up: Relativity and Electromagnetism
Previous: Electromagnetic Energy Tensor
Let us calculate the electric and magnetic fields observed at position
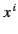 and time
and time 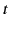 due to a charge
due to a charge 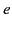 whose retarded position and
time are
whose retarded position and
time are 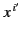 and
and 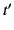 , respectively. From now on
, respectively. From now on
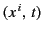 is termed
the field point and
is termed
the field point and
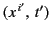 is termed the source point.
It is assumed that we are given the retarded position of the charge as
a function of its retarded time: i.e.,
is termed the source point.
It is assumed that we are given the retarded position of the charge as
a function of its retarded time: i.e.,
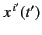 . The retarded
velocity and acceleration of the charge are
. The retarded
velocity and acceleration of the charge are
 |
(1889) |
and
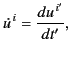 |
(1890) |
respectively. The radius vector  is defined to extend
from the retarded position of the charge to the field point,
so that
is defined to extend
from the retarded position of the charge to the field point,
so that
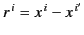 .
(Note that this is the opposite convention to that adopted in Sections 12.18
and 12.19). It follows that
.
(Note that this is the opposite convention to that adopted in Sections 12.18
and 12.19). It follows that
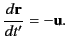 |
(1891) |
The field and the source point variables are connected by the retardation
condition
![$\displaystyle r(x^{\,i}, x^{\,i'}) = \left[ (x^{\,i}-x^{\,i'})\,(x_{\,i}-x_{\,i'})\right]^{1/2} = c\,(t-t').$](img3988.png) |
(1892) |
The potentials generated by the charge are given by the Liénard-Wiechert
formulae,
where
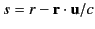 is a function both of
the field point and the source point variables. Recall that the Liénard-Wiechert potentials are valid for
accelerating, as well as uniformly moving, charges.
is a function both of
the field point and the source point variables. Recall that the Liénard-Wiechert potentials are valid for
accelerating, as well as uniformly moving, charges.
The fields  and
and  are derived from the potentials
in the usual manner:
are derived from the potentials
in the usual manner:
However, the components of the gradient operator 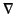 are partial
derivatives at constant time,
are partial
derivatives at constant time, 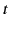 , and not at constant time,
, and not at constant time, 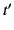 .
Partial differentiation with respect to the
.
Partial differentiation with respect to the 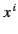 compares the potentials at neighboring points at the same time, but these potential signals originate from the charge at different retarded times.
Similarly, the partial derivative with respect to
compares the potentials at neighboring points at the same time, but these potential signals originate from the charge at different retarded times.
Similarly, the partial derivative with respect to 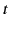 implies
constant
implies
constant 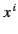 , and, hence, refers to the comparison of the potentials at
a given field point over an interval of time during which the retarded
coordinates of the source have changed. Because we only know the time variation
of the particle's retarded position with respect to
, and, hence, refers to the comparison of the potentials at
a given field point over an interval of time during which the retarded
coordinates of the source have changed. Because we only know the time variation
of the particle's retarded position with respect to 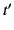 we must
transform
we must
transform
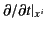 and
and
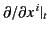 to
expressions involving
to
expressions involving
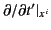 and
and
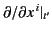 .
.
Now, because 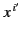 is assumed to be given as a function of
is assumed to be given as a function of 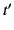 ,
we have
,
we have
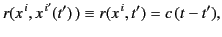 |
(1897) |
which is a functional relationship between 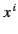 ,
, 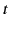 , and
, and 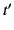 .
Note that
.
Note that
 |
(1898) |
It follows that
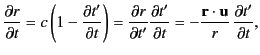 |
(1899) |
where all differentiation is at constant 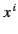 . Thus,
. Thus,
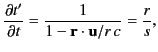 |
(1900) |
giving
 |
(1901) |
Similarly,
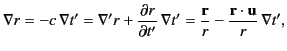 |
(1902) |
where 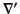 denotes differentiation with respect to
denotes differentiation with respect to 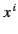 at constant
at constant
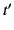 . It follows that
. It follows that
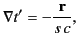 |
(1903) |
so that
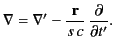 |
(1904) |
Equation (1897) yields
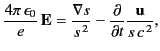 |
(1905) |
or
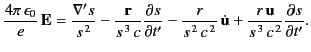 |
(1906) |
However,
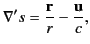 |
(1907) |
and
 |
(1908) |
Thus,
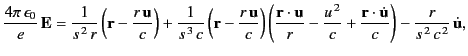 |
(1909) |
which reduces to
![$\displaystyle \frac{4\pi \,\epsilon_0}{e}\, {\bf E} = \frac{1}{s^{\,3}} \left({...
...t[ \left({\bf r} - \frac{r\,{\bf u}}{c}\right)\times\dot{\bf u}\right] \right).$](img4011.png) |
(1910) |
Similarly,
 |
(1911) |
or
![$\displaystyle \frac{4\pi}{\mu_0\,e}\, {\bf B} = -\frac{{\bf r}\times{\bf u}}{s^...
...f u}}{r} + \frac{{\bf r}\cdot\dot{\bf u}}{c} - \frac{u^{\,2}}{c}\right)\right],$](img4013.png) |
(1912) |
which reduces to
![$\displaystyle \frac{4\pi}{\mu_0\,e}\, {\bf B} = \frac{{\bf u}\times{\bf r}}{s^{...
...t[ \left({\bf r} - \frac{r\,{\bf u}}{c}\right)\times\dot{\bf u}\right] \right).$](img4014.png) |
(1913) |
A comparison of Equations (1912) and (1915) yields
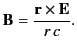 |
(1914) |
Thus, the magnetic field is always perpendicular to  and the
retarded radius vector
and the
retarded radius vector  . Note that all terms appearing in
the previous formulae are retarded.
. Note that all terms appearing in
the previous formulae are retarded.
The electric field is composed of two separate parts. The first term
in Equation (1912) varies as 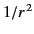 for large distances from the charge.
We can think of
for large distances from the charge.
We can think of
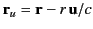 as the virtual present radius vector:
that is, the radius vector directed from the position
the charge would occupy at time
as the virtual present radius vector:
that is, the radius vector directed from the position
the charge would occupy at time 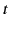 if it had continued with
uniform velocity from its retarded position to the field point.
In terms of
if it had continued with
uniform velocity from its retarded position to the field point.
In terms of 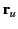 , the
, the 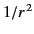 field is simply
field is simply
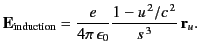 |
(1915) |
We can rewrite the expression (1835) for the electric field generated
by a uniformly moving charge in the form
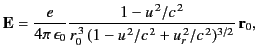 |
(1916) |
where 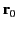 is the radius vector directed from the present
position of the charge at time
is the radius vector directed from the present
position of the charge at time 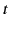 to the field point, and
to the field point, and
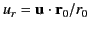 . For the case of uniform motion,
the relationship between the retarded radius vector
. For the case of uniform motion,
the relationship between the retarded radius vector  and
the actual radius vector
and
the actual radius vector 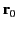 is simply
is simply
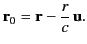 |
(1917) |
It is straightforward to demonstrate that
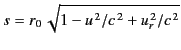 |
(1918) |
in this case. Thus, the electric field generated by a uniformly
moving charge can be written
 |
(1919) |
Because
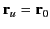 for the case of a uniformly moving charge,
it is clear that Equation (1917) is equivalent to the electric field generated
by a uniformly moving charge located at the position the charge would occupy
if it had continued with uniform velocity from its retarded position.
for the case of a uniformly moving charge,
it is clear that Equation (1917) is equivalent to the electric field generated
by a uniformly moving charge located at the position the charge would occupy
if it had continued with uniform velocity from its retarded position.
The second term in Equation (1912),
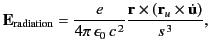 |
(1920) |
is of order 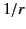 , and, therefore, represents a radiation field. Similar
considerations hold for the two terms of Equation (1915).
, and, therefore, represents a radiation field. Similar
considerations hold for the two terms of Equation (1915).



Next: Larmor Formula
Up: Relativity and Electromagnetism
Previous: Electromagnetic Energy Tensor
Richard Fitzpatrick
2014-06-27


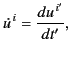
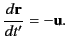

![]() and
and ![]() are derived from the potentials
in the usual manner:
are derived from the potentials
in the usual manner:
![]() is assumed to be given as a function of
is assumed to be given as a function of ![]() ,
we have
,
we have

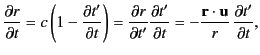

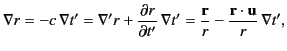
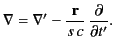
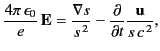
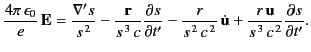

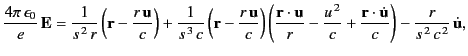

![$\displaystyle \frac{4\pi}{\mu_0\,e}\, {\bf B} = -\frac{{\bf r}\times{\bf u}}{s^...
...f u}}{r} + \frac{{\bf r}\cdot\dot{\bf u}}{c} - \frac{u^{\,2}}{c}\right)\right],$](img4013.png)
![]() for large distances from the charge.
We can think of
for large distances from the charge.
We can think of
![]() as the virtual present radius vector:
that is, the radius vector directed from the position
the charge would occupy at time
as the virtual present radius vector:
that is, the radius vector directed from the position
the charge would occupy at time ![]() if it had continued with
uniform velocity from its retarded position to the field point.
In terms of
if it had continued with
uniform velocity from its retarded position to the field point.
In terms of ![]() , the
, the ![]() field is simply
field is simply