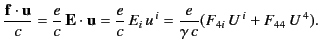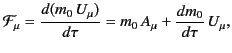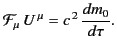Next: Electromagnetic Energy Tensor
Up: Relativity and Electromagnetism
Previous: Relativistic Particle Dynamics
The electromagnetic 3-force acting on a charge 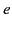 moving with 3-velocity
moving with 3-velocity
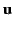 is given by the well-known formula
is given by the well-known formula
 |
(1851) |
When written in component form this expression becomes
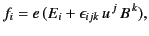 |
(1852) |
or
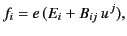 |
(1853) |
where use has been made of Equation (1766).
Recall that the components of the  and
and  fields can be written
in terms of an antisymmetric electromagnetic field tensor
fields can be written
in terms of an antisymmetric electromagnetic field tensor
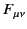 via
via
Equation (1855) can be written
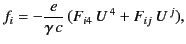 |
(1856) |
where
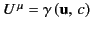 is the particle's 4-velocity.
It is easily demonstrated that
is the particle's 4-velocity.
It is easily demonstrated that
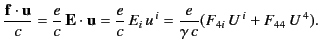 |
(1857) |
Thus, the 4-force acting on the particle,
 |
(1858) |
can be written in the form
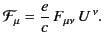 |
(1859) |
The skew symmetry of the electromagnetic field tensor ensures that
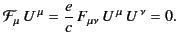 |
(1860) |
This is an important result, because it ensures that electromagnetic fields
do not change the rest mass of charged particles. In order to appreciate this,
let us assume that the rest mass 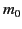 is not a constant.
Because
is not a constant.
Because
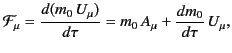 |
(1861) |
we can use the standard results
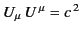 and
and
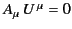 to give
to give
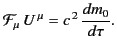 |
(1862) |
Thus, if rest mass is to remain an invariant, it is imperative that
all laws of physics predict 4-forces acting on particles that
are orthogonal to the particles' instantaneous 4-velocities. The laws of electromagnetism
pass this test.



Next: Electromagnetic Energy Tensor
Up: Relativity and Electromagnetism
Previous: Relativistic Particle Dynamics
Richard Fitzpatrick
2014-06-27
![]() and
and ![]() fields can be written
in terms of an antisymmetric electromagnetic field tensor
fields can be written
in terms of an antisymmetric electromagnetic field tensor
![]() via
via