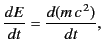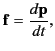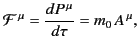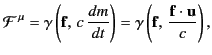Next: Force on a Moving
Up: Relativity and Electromagnetism
Previous: Field Due to a
Consider a particle that, in its instantaneous rest frame 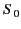 , has
mass
, has
mass 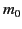 and constant acceleration in the
and constant acceleration in the  -direction
-direction  .
Let us transform to a frame
.
Let us transform to a frame  , in the standard configuration with respect
to
, in the standard configuration with respect
to 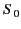 , in which the particle's instantaneous
velocity is
, in which the particle's instantaneous
velocity is 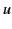 . What is the value of
. What is the value of 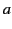 , the
particle's instantaneous
, the
particle's instantaneous  -acceleration, in
S?
-acceleration, in
S?
The easiest way in which to answer this question is to consider the
acceleration 4-vector [see Equation (1726)]
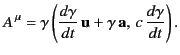 |
(1836) |
Using the standard transformation, (1694)-(1697), for 4-vectors, we obtain
Equation (1839) can be written
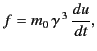 |
(1839) |
where
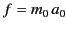 is the constant
force (in the
is the constant
force (in the  -direction) acting on the particle in
-direction) acting on the particle in 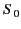 .
.
Equation (1841) is equivalent to
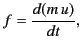 |
(1840) |
where
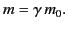 |
(1841) |
Thus, we can account for the ever decreasing acceleration of a particle
subject to a constant force [see Equation (1839)] by supposing that the
inertial mass of the particle increases with its velocity according to
the rule (1843). Henceforth, 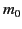 is termed the rest mass, and
is termed the rest mass, and
 the inertial mass.
the inertial mass.
The rate of increase of the particle's energy 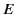 satisfies
satisfies
 |
(1842) |
This equation can be written
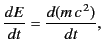 |
(1843) |
which can be integrated to yield Einstein's famous formula
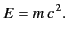 |
(1844) |
The 3-momentum of a particle is defined
 |
(1845) |
where 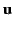 is its 3-velocity. Thus, by analogy with Equation (1842),
Newton's law of motion can be written
is its 3-velocity. Thus, by analogy with Equation (1842),
Newton's law of motion can be written
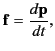 |
(1846) |
where 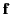 is the 3-force acting on the particle.
is the 3-force acting on the particle.
The 4-momentum of a particle is defined
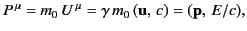 |
(1847) |
where  is its 4-velocity. The 4-force acting on the particle
obeys
is its 4-velocity. The 4-force acting on the particle
obeys
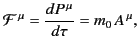 |
(1848) |
where  is its 4-acceleration. It is easily demonstrated that
is its 4-acceleration. It is easily demonstrated that
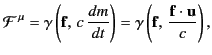 |
(1849) |
because
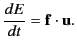 |
(1850) |



Next: Force on a Moving
Up: Relativity and Electromagnetism
Previous: Field Due to a
Richard Fitzpatrick
2014-06-27
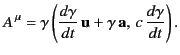
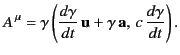
![]() satisfies
satisfies