


Next: Separation of variables
Up: Electrostatics
Previous: The method of images
Let us now investigate another trick for solving Poisson's equation (actually
it only solves Laplace's equation).
Unfortunately, this method can only be applied in two dimensions.
The complex variable is conventionally written
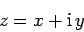 |
(740) |
( should not be confused with a
should not be confused with a  -coordinate: this is a strictly two-dimensional problem). We can write functions
-coordinate: this is a strictly two-dimensional problem). We can write functions  of the complex variable just like
we would write functions of a real variable. For instance,
of the complex variable just like
we would write functions of a real variable. For instance,
For a given function,  , we can substitute
, we can substitute
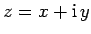 and write
and write
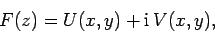 |
(743) |
where 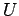 and
and  are two real two-dimensional functions. Thus, if
are two real two-dimensional functions. Thus, if
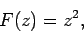 |
(744) |
then
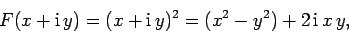 |
(745) |
giving
We can define the derivative of a complex function in just the same manner as
we would define the derivative of a real function. Thus,
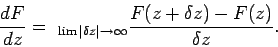 |
(748) |
However, we now have a slight problem. If  is a ``well-defined''
function (we shall leave it to the mathematicians to specify exactly what
being well-defined entails: suffice to say that most functions we can think
of are well-defined) then it should not matter from which direction in the complex
plane we approach
is a ``well-defined''
function (we shall leave it to the mathematicians to specify exactly what
being well-defined entails: suffice to say that most functions we can think
of are well-defined) then it should not matter from which direction in the complex
plane we approach  when taking the limit in Eq. (748).
There are, of course, many
different directions we could approach
when taking the limit in Eq. (748).
There are, of course, many
different directions we could approach  from, but if we look at a regular complex
function,
from, but if we look at a regular complex
function, 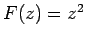 (say), then
(say), then
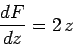 |
(749) |
is perfectly well-defined, and is, therefore, completely independent of the details of
how the limit is taken in Eq. (748).
The fact that Eq. (748)
has to give the same result, no matter which path we approach
 from, means that there are some restrictions on the functions
from, means that there are some restrictions on the functions 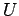 and
and  in
Eq. (743).
Suppose that we approach
in
Eq. (743).
Suppose that we approach  along the real axis, so that
along the real axis, so that
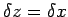 .
Then,
.
Then,
Suppose that we now approach  along the imaginary axis, so that
along the imaginary axis, so that
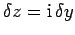 . Then,
. Then,
If  is a well-defined function then its derivative must also be
well-defined,
which implies that the above two expressions are equivalent. This
requires that
is a well-defined function then its derivative must also be
well-defined,
which implies that the above two expressions are equivalent. This
requires that
These are called the Cauchy-Riemann relations, and are, in fact, sufficient to ensure
that all possible ways of taking the limit (748) give the same answer.
So far, we have found that a general complex function  can be written
can be written
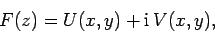 |
(754) |
where
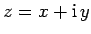 . If
. If  is well-defined then
is well-defined then 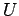 and
and  automatically satisfy the Cauchy-Riemann relations.
But, what has all of this got to do with electrostatics? Well, we can combine the
two Cauchy-Riemann relations. We get
automatically satisfy the Cauchy-Riemann relations.
But, what has all of this got to do with electrostatics? Well, we can combine the
two Cauchy-Riemann relations. We get
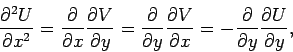 |
(755) |
and
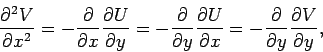 |
(756) |
which reduce to
Thus, both 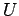 and
and  automatically satisfy Laplace's equation in
two dimensions; i.e., both
automatically satisfy Laplace's equation in
two dimensions; i.e., both 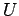 and
and  are possible two-dimensional scalar potentials
in free space.
are possible two-dimensional scalar potentials
in free space.
Consider the two-dimensional gradients of 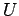 and
and  :
:
Now
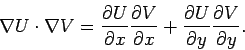 |
(761) |
It follows from the Cauchy-Riemann relations that
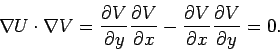 |
(762) |
Thus, the contours of 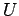 are everywhere perpendicular to the contours of
are everywhere perpendicular to the contours of  .
It follows that if
.
It follows that if 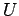 maps out the contours of some free space scalar potential
then
maps out the contours of some free space scalar potential
then  indicates the directions of the associated electric field-lines,
and vice versa.
indicates the directions of the associated electric field-lines,
and vice versa.
Figure 45:
 |
For every well-defined complex function we can think of, we get two sets
of free space potentials, and the associated electric field-lines. For example,
consider the function 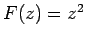 , for which
, for which
These are, in fact, the equations of two sets of orthogonal hyperboloids.
So, 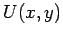 (the solid lines in Fig. 45)
might represent the contours of some scalar potential and
(the solid lines in Fig. 45)
might represent the contours of some scalar potential and 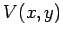 (the dashed lines in Fig. 45)
the associated electric field lines, or vice versa. But, how could we
actually generate a hyperboloidal potential? This is easy. Consider the contours
of
(the dashed lines in Fig. 45)
the associated electric field lines, or vice versa. But, how could we
actually generate a hyperboloidal potential? This is easy. Consider the contours
of 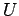 at level
at level 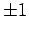 . These could represent the surfaces of four hyperboloid
conductors maintained at potentials
. These could represent the surfaces of four hyperboloid
conductors maintained at potentials 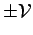 . The scalar potential in the
region between these conductors is given by
. The scalar potential in the
region between these conductors is given by
 , and the associated
electric field-lines follow the contours of
, and the associated
electric field-lines follow the contours of 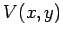 .
Note that
.
Note that
 |
(765) |
Thus, the  -component of the electric
field is directly proportional to the distance
from the
-component of the electric
field is directly proportional to the distance
from the  -axis. Likewise, for
-axis. Likewise, for  -component of the field is directly proportional
to the distance from the
-component of the field is directly proportional
to the distance from the  -axis. This property
can be exploited to make devices (called quadrupole electrostatic lenses) which
are useful for focusing particle beams.
-axis. This property
can be exploited to make devices (called quadrupole electrostatic lenses) which
are useful for focusing particle beams.
As a second example, consider the complex function
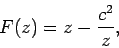 |
(766) |
where 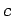 is real and positive. Writing
is real and positive. Writing
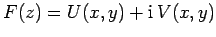 , we find that
, we find that
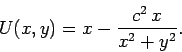 |
(767) |
Far from the origin,
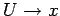 , which is the potential of a
uniform electric field, of unit amplitude, pointing in the
, which is the potential of a
uniform electric field, of unit amplitude, pointing in the 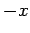 -direction. The locus
of
-direction. The locus
of 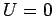 is
is 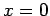 , and
, and
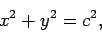 |
(768) |
which corresponds to a circle of radius 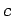 centered on the origin. Hence,
we conclude that the potential
centered on the origin. Hence,
we conclude that the potential
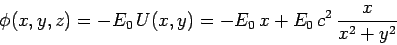 |
(769) |
corresponds to that outside a grounded, infinitely long, conducting cylinder of radius 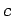 , running parallel
to the
, running parallel
to the  -axis, placed in a uniform
-axis, placed in a uniform  -directed electric field of
magnitude
-directed electric field of
magnitude 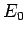 . Of course, the potential inside the cylinder (i.e.,
. Of course, the potential inside the cylinder (i.e.,
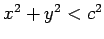 ) is zero. The induced charge density on the surface of
the cylinder is simply
) is zero. The induced charge density on the surface of
the cylinder is simply
 |
(770) |
where 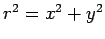 , and
, and
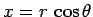 . Note that zero
net charge is induced on the surface.
. Note that zero
net charge is induced on the surface.
We can think of the set of all possible well-defined complex functions as a
reference library of solutions to Laplace's equation in two
dimensions. We have only considered a couple of examples, but there are, of course,
very many complex functions which generate interesting potentials.
For instance,
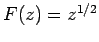 generates the potential around a semi-infinite,
thin, grounded, conducting plate placed
in an external field, whereas
generates the potential around a semi-infinite,
thin, grounded, conducting plate placed
in an external field, whereas
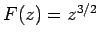 yields the potential outside a
grounded, rectangular, conducting corner under similar circumstances.
yields the potential outside a
grounded, rectangular, conducting corner under similar circumstances.



Next: Separation of variables
Up: Electrostatics
Previous: The method of images
Richard Fitzpatrick
2006-02-02
![]() from, means that there are some restrictions on the functions
from, means that there are some restrictions on the functions ![]() and
and ![]() in
Eq. (743).
Suppose that we approach
in
Eq. (743).
Suppose that we approach ![]() along the real axis, so that
along the real axis, so that
![]() .
Then,
.
Then,
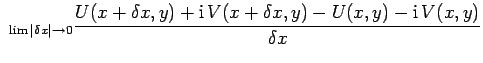
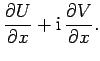

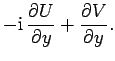
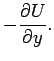
![]() can be written
can be written
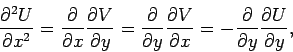
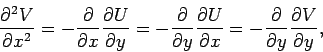

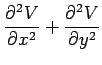
![]() and
and ![]() :
:
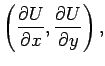

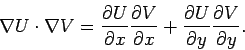
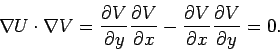
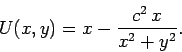
![]() generates the potential around a semi-infinite,
thin, grounded, conducting plate placed
in an external field, whereas
generates the potential around a semi-infinite,
thin, grounded, conducting plate placed
in an external field, whereas
![]() yields the potential outside a
grounded, rectangular, conducting corner under similar circumstances.
yields the potential outside a
grounded, rectangular, conducting corner under similar circumstances.