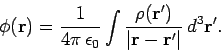Next: Ampère's experiments
Up: Time-independent Maxwell equations
Previous: Gauss' law
We have seen that the electric field generated by a set of stationary charges can be written as
the gradient of a scalar potential, so that
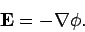 |
(218) |
This equation can be combined with the field equation (213) to give a partial
differential equation for the scalar potential:
 |
(219) |
This is an example of a very famous type of partial differential equation known
as Poisson's equation.
In its most general form, Poisson's equation is written
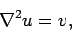 |
(220) |
where 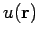 is some scalar potential which is
to be determined, and
is some scalar potential which is
to be determined, and
 is a known ``source function.'' The most common boundary condition
applied to this equation is that the potential
is a known ``source function.'' The most common boundary condition
applied to this equation is that the potential 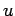 is zero at infinity.
The solutions to Poisson's equation are completely superposable. Thus, if
is zero at infinity.
The solutions to Poisson's equation are completely superposable. Thus, if
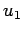 is the potential generated by the source function
is the potential generated by the source function 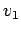 , and
, and
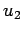 is the potential generated by the source function
is the potential generated by the source function 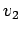 , so that
, so that
 |
(221) |
then the potential generated by 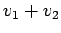 is
is  , since
, since
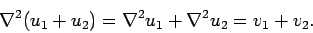 |
(222) |
Poisson's equation has this property because it is linear in both the
potential and the source term.
The fact that the solutions to Poisson's equation are superposable suggests a
general method for solving this equation. Suppose that we could construct all
of the solutions
generated by point sources. Of course, these solutions
must satisfy the appropriate boundary conditions.
Any general source function can be built up out of a set of suitably weighted
point sources, so the general solution of Poisson's equation must be
expressible as a weighted sum over the point source solutions. Thus, once we
know all of the point source solutions we can construct any other solution.
In mathematical terminology, we require the solution to
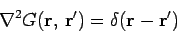 |
(223) |
which goes to zero as
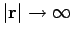 . The function
. The function
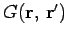 is the solution generated by a unit point source located at position
is the solution generated by a unit point source located at position 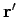 .
This function is known to mathematicians as a Green's function. The solution
generated by a general source function
.
This function is known to mathematicians as a Green's function. The solution
generated by a general source function  is simply the
appropriately weighted sum of
all of the Green's function solutions:
is simply the
appropriately weighted sum of
all of the Green's function solutions:
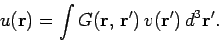 |
(224) |
We can easily demonstrate that this is the correct solution:
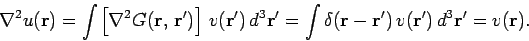 |
(225) |
Let us return to Eq. (219):
 |
(226) |
The Green's function for this equation satisfies Eq. (223) with
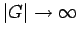 as
as
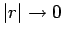 . It follows from Eq. (215) that
. It follows from Eq. (215) that
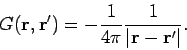 |
(227) |
Note, from Eq. (180), that the Green's function has the same form as the potential
generated by a point charge. This is hardly surprising, given the definition of
a Green's function. It follows from Eq. (224) and (227) that the general solution
to Poisson's equation, (226), is written
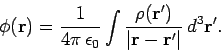 |
(228) |
In fact, we have already obtained this solution by another method [see Eq. (177)].



Next: Ampère's experiments
Up: Time-independent Maxwell equations
Previous: Gauss' law
Richard Fitzpatrick
2006-02-02