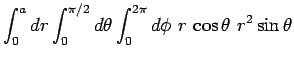Next: Gradient
Up: Vectors
Previous: Vector surface integrals
A volume integral takes the form
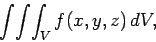 |
(89) |
where  is some volume, and
is some volume, and
 is a small volume element. The
volume element is sometimes written
is a small volume element. The
volume element is sometimes written 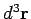 , or even
, or even 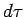 . As an example
of a volume integral, let us evaluate the centre of gravity of a solid hemisphere
of radius
. As an example
of a volume integral, let us evaluate the centre of gravity of a solid hemisphere
of radius  (centered on the origin).
The height of the centre of gravity is given by
(centered on the origin).
The height of the centre of gravity is given by
 |
(90) |
The bottom integral is simply the volume of the hemisphere, which is  .
The top integral is most easily evaluated in spherical polar coordinates, for which
.
The top integral is most easily evaluated in spherical polar coordinates, for which
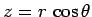 and
and
 . Thus,
. Thus,
giving
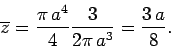 |
(92) |



Next: Gradient
Up: Vectors
Previous: Vector surface integrals
Richard Fitzpatrick
2006-02-02