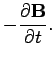Next: Transformation of fields
Up: Relativity and electromagnetism
Previous: The electromagnetic field tensor
We have seen that it is possible to write the components of
the electric and magnetic fields as the components of a proper-4-tensor.
Is it also possible to write the components of these fields as the components
of some pseudo-4-tensor? It is obvious that we cannot identify
the components of
the proper-3-vector 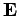 with any of the components of a
pseudo-tensor. However, we can represent the components of
with any of the components of a
pseudo-tensor. However, we can represent the components of 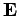 in terms of those of an antisymmetric pseudo-3-tensor
in terms of those of an antisymmetric pseudo-3-tensor 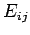 by writing
by writing
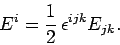 |
(1491) |
It is easily demonstrated that
![\begin{displaymath}
E^{ij}=E_{ij} = \left(\begin{array}{ccc}
0& E_z & -E_y\ [0....
...
-E_z & 0 & E_x \ [0.5ex]
E_y & -E_x & 0 \end{array} \right),
\end{displaymath}](img3057.png) |
(1492) |
in a right-handed coordinate system.
Consider the dual electromagnetic field tensor, 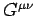 ,
which is defined
,
which is defined
 |
(1493) |
This tensor is clearly an antisymmetric pseudo-4-tensor. We have
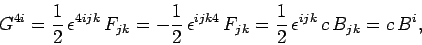 |
(1494) |
plus
 |
(1495) |
where use has been made of
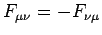 . The above
expression yields
. The above
expression yields
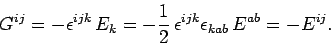 |
(1496) |
It follows that
or
![\begin{displaymath}
G^{\mu\nu} = \left\lgroup \begin{array}{cccc}
0 & -E_z & +E_...
....5ex]
+c B_x &+ c B_y &+c B_z & 0\end{array}\right
\rgroup.
\end{displaymath}](img3068.png) |
(1499) |
The above expression is, again, slightly misleading, since
 stands for the component
stands for the component 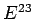 of the pseudo-3-tensor
of the pseudo-3-tensor  ,
and not for an element of the proper-3-vector
,
and not for an element of the proper-3-vector 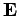 . Of course,
in this case,
. Of course,
in this case, 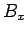 really does represent
the first element of the pseudo-3-vector
really does represent
the first element of the pseudo-3-vector
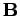 .
Note that the elements of
.
Note that the elements of 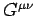 are obtained from those of
are obtained from those of  by making the transformation
by making the transformation
 and
and
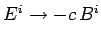 .
.
The covariant elements of the dual electromagnetic field tensor are
given by
or
![\begin{displaymath}
G_{\mu\nu} = \left\lgroup \begin{array}{cccc}
0 & -E_z & +E_...
....5ex]
-c B_x & -c B_y &-c B_z & 0\end{array}\right
\rgroup.
\end{displaymath}](img3079.png) |
(1502) |
The elements of 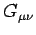 are obtained from those of
are obtained from those of  by making the transformation
by making the transformation
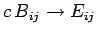 and
and
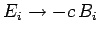 .
.
Let us now consider the two Maxwell equations
The first of these equations can be written
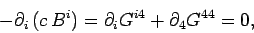 |
(1505) |
since 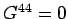 . The second equation takes the form
. The second equation takes the form
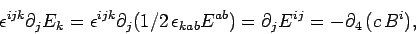 |
(1506) |
or
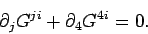 |
(1507) |
Equations (1505) and (1507) can be combined to give
 |
(1508) |
Thus, we conclude that Maxwell's equations for the electromagnetic fields
are equivalent to the following pair of 4-tensor equations:
It is obvious from the form of these equations that the laws of electromagnetism
are invariant under translations, rotations, special Lorentz transformations,
parity inversions, or any combination of these transformations.



Next: Transformation of fields
Up: Relativity and electromagnetism
Previous: The electromagnetic field tensor
Richard Fitzpatrick
2006-02-02
![\begin{displaymath}
E^{ij}=E_{ij} = \left(\begin{array}{ccc}
0& E_z & -E_y\ [0....
...
-E_z & 0 & E_x \ [0.5ex]
E_y & -E_x & 0 \end{array} \right),
\end{displaymath}](img3057.png)
![]() ,
which is defined
,
which is defined
![\begin{displaymath}
G^{\mu\nu} = \left\lgroup \begin{array}{cccc}
0 & -E_z & +E_...
....5ex]
+c B_x &+ c B_y &+c B_z & 0\end{array}\right
\rgroup.
\end{displaymath}](img3068.png)
![\begin{displaymath}
G_{\mu\nu} = \left\lgroup \begin{array}{cccc}
0 & -E_z & +E_...
....5ex]
-c B_x & -c B_y &-c B_z & 0\end{array}\right
\rgroup.
\end{displaymath}](img3079.png)