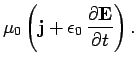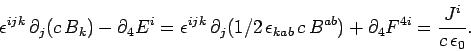Next: The dual electromagnetic field
Up: Relativity and electromagnetism
Previous: Tensors and pseudo-tensors
Let us now investigate whether we can write the components of
the electric and magnetic
fields as the components of some proper 4-tensor. There
is an obvious problem here. How can we identify the components
of the magnetic
field, which is a pseudo-vector, with any of the components of a
proper-4-tensor? The former components transform differently under parity inversion
than the latter components.
Consider a proper-3-tensor whose
covariant components are written  , and which is
antisymmetric:
, and which is
antisymmetric:
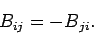 |
(1467) |
This immediately implies that all of the diagonal components of the
tensor are zero. In fact, there are only three independent non-zero
components of such a tensor. Could we, perhaps, use these components to
represent the components of a pseudo-3-vector? Let us write
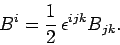 |
(1468) |
It is clear that 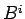 transforms as a contravariant pseudo-3-vector.
It is easily seen that
transforms as a contravariant pseudo-3-vector.
It is easily seen that
![\begin{displaymath}
B^{ij}=B_{ij} = \left(\begin{array}{ccc}
0& B_z & -B_y\ [0....
...
-B_z & 0 & B_x \ [0.5ex]
B_y & -B_x & 0 \end{array} \right),
\end{displaymath}](img3019.png) |
(1469) |
where
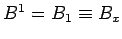 , etc. In this manner, we can actually
write the components of a pseudo-3-vector as the components of an
antisymmetric
proper-3-tensor. In particular, we can write the components of the magnetic field
, etc. In this manner, we can actually
write the components of a pseudo-3-vector as the components of an
antisymmetric
proper-3-tensor. In particular, we can write the components of the magnetic field 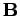 in terms of
an antisymmetric
proper magnetic field 3-tensor which we shall denote
in terms of
an antisymmetric
proper magnetic field 3-tensor which we shall denote 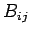 .
.
Let us now examine Eqs. (1465) and (1466) more carefully. Recall that
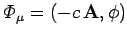 and
and
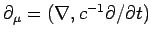 . It follows that we can write
Eq. (1465) in the form
. It follows that we can write
Eq. (1465) in the form
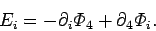 |
(1470) |
Likewise, Eq. (1466) can be written
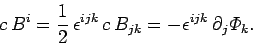 |
(1471) |
Let us multiply this expression by
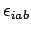 , making use of the
identity
, making use of the
identity
 |
(1472) |
We obtain
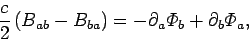 |
(1473) |
or
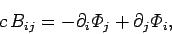 |
(1474) |
since
 .
.
Let us define a proper-4-tensor whose covariant
components are given by
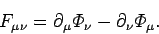 |
(1475) |
It is clear that this tensor is antisymmetric:
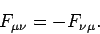 |
(1476) |
This implies that the tensor only possesses six independent non-zero
components. Maybe it can be used to specify the components of 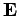 and
and 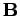 ?
?
Equations (1470) and (1475) yield
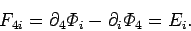 |
(1477) |
Likewise, Eqs. (1474) and (1475) imply that
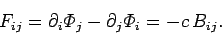 |
(1478) |
Thus,
In other words, the completely space-like components of the tensor specify
the components of the magnetic field, whereas the hybrid space and time-like
components specify the components of the electric field. The covariant
components
of the tensor can be written
![\begin{displaymath}
F_{\mu\nu} = \left\lgroup \begin{array}{cccc}
0 & -c B_z & ...
...-E_z\ [0.5ex]
+E_x & +E_y &+E_z & 0\end{array}\right
\rgroup.
\end{displaymath}](img3038.png) |
(1481) |
Not surprisingly,  is usually called the electromagnetic
field tensor.
The above expression, which appears in all standard textbooks, is very
misleading. Taken at face value, it is simply wrong! We cannot form
a proper-4-tensor from the components of a proper-3-vector and a pseudo-3-vector. The expression only makes sense if we interpret
is usually called the electromagnetic
field tensor.
The above expression, which appears in all standard textbooks, is very
misleading. Taken at face value, it is simply wrong! We cannot form
a proper-4-tensor from the components of a proper-3-vector and a pseudo-3-vector. The expression only makes sense if we interpret 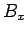 (say) as representing the component
(say) as representing the component 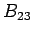 of the proper magnetic field 3-tensor
of the proper magnetic field 3-tensor 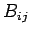
The
contravariant components of the electromagnetic field tensor
are given by
or
![\begin{displaymath}
F^{\mu\nu} = \left\lgroup \begin{array}{cccc}
0 & -c B_z & ...
...+E_z\ [0.5ex]
-E_x & -E_y &-E_z & 0\end{array}\right
\rgroup.
\end{displaymath}](img3046.png) |
(1484) |
Let us now consider two of Maxwell's equations:
Recall that the 4-current is defined
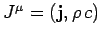 .
The first of these equations can be written
.
The first of these equations can be written
 |
(1487) |
since  .
The second of these equations takes the form
.
The second of these equations takes the form
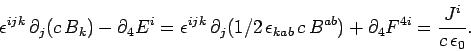 |
(1488) |
Making use of Eq. (1472), the above expression reduces to
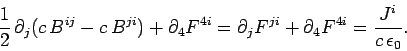 |
(1489) |
Equations (1487) and (1489) can be combined to give
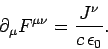 |
(1490) |
This equation is consistent with the equation of charge
continuity,
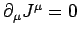 , because of the antisymmetry of
the electromagnetic field tensor.
, because of the antisymmetry of
the electromagnetic field tensor.



Next: The dual electromagnetic field
Up: Relativity and electromagnetism
Previous: Tensors and pseudo-tensors
Richard Fitzpatrick
2006-02-02
![]() and
and
![]() . It follows that we can write
Eq. (1465) in the form
. It follows that we can write
Eq. (1465) in the form