


Next: The scalar triple product
Up: Vectors
Previous: The vector product
Let us try to define a rotation vector 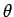 whose magnitude
is the angle of the rotation,
whose magnitude
is the angle of the rotation, 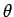 , and whose direction is the axis of the
rotation, in the sense determined by the right-hand grip rule. Is this a good
vector? The short answer is, no. The problem is that the addition of rotations
is not commutative, whereas vector addition is commuative.
Figure 9 shows the effect of applying two successive
, and whose direction is the axis of the
rotation, in the sense determined by the right-hand grip rule. Is this a good
vector? The short answer is, no. The problem is that the addition of rotations
is not commutative, whereas vector addition is commuative.
Figure 9 shows the effect of applying two successive 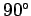 rotations,
one about
rotations,
one about  -axis, and the other about the
-axis, and the other about the  -axis, to a six-sided die. In the
left-hand case, the
-axis, to a six-sided die. In the
left-hand case, the  -rotation is applied before the
-rotation is applied before the  -rotation, and vice
versa in the right-hand case. It can be seen that the die ends up in two completely
different states. Clearly, the
-rotation, and vice
versa in the right-hand case. It can be seen that the die ends up in two completely
different states. Clearly, the  -rotation plus the
-rotation plus the
 -rotation does not equal
the
-rotation does not equal
the  -rotation plus the
-rotation plus the  -rotation. This non-commuting algebra cannot be
represented by vectors. So, although rotations have a well-defined magnitude and
direction, they are not vector quantities.
-rotation. This non-commuting algebra cannot be
represented by vectors. So, although rotations have a well-defined magnitude and
direction, they are not vector quantities.
Figure 9:
![\begin{figure}
\epsfysize =4in
\centerline{\epsffile[-300 -40 860 771]{figx9.ps}}
\end{figure}](img156.png) |
But, this is not quite the end of the story. Suppose that we take a general vector
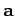 and rotate it about the
and rotate it about the  -axis by a small angle
-axis by a small angle
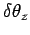 .
This is equivalent to rotating the basis about the
.
This is equivalent to rotating the basis about the  -axis by
-axis by
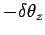 .
According to Eqs. (10)-(12), we have
.
According to Eqs. (10)-(12), we have
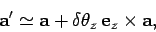 |
(39) |
where use has been made of the small angle expansions
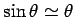 and
and
 . The above equation can easily be generalized to allow
small rotations about the
. The above equation can easily be generalized to allow
small rotations about the  - and
- and  -axes by
-axes by
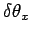 and
and
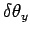 ,
respectively. We find that
,
respectively. We find that
 |
(40) |
where
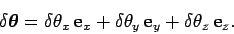 |
(41) |
Clearly, we can define a rotation vector 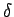
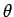 , but it only
works for small angle rotations (i.e., sufficiently small that the small
angle expansions of sine and cosine are good). According to the above equation,
a small
, but it only
works for small angle rotations (i.e., sufficiently small that the small
angle expansions of sine and cosine are good). According to the above equation,
a small  -rotation plus a small
-rotation plus a small  -rotation is (approximately) equal to
the two rotations applied in the opposite order.
The fact that infinitesimal rotation is a vector implies that angular velocity,
-rotation is (approximately) equal to
the two rotations applied in the opposite order.
The fact that infinitesimal rotation is a vector implies that angular velocity,
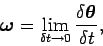 |
(42) |
must be a vector as well. Also, if 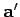 is interpreted as
is interpreted as
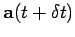 in the above equation then it is clear that the equation of motion of a vector
precessing about the origin with angular velocity
in the above equation then it is clear that the equation of motion of a vector
precessing about the origin with angular velocity 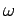 is
is
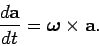 |
(43) |



Next: The scalar triple product
Up: Vectors
Previous: The vector product
Richard Fitzpatrick
2006-02-02
![\begin{figure}
\epsfysize =4in
\centerline{\epsffile[-300 -40 860 771]{figx9.ps}}
\end{figure}](img156.png)
![]() and rotate it about the
and rotate it about the ![]() -axis by a small angle
-axis by a small angle
![]() .
This is equivalent to rotating the basis about the
.
This is equivalent to rotating the basis about the ![]() -axis by
-axis by
![]() .
According to Eqs. (10)-(12), we have
.
According to Eqs. (10)-(12), we have