


Next: Vector areas
Up: Vectors
Previous: Introduction
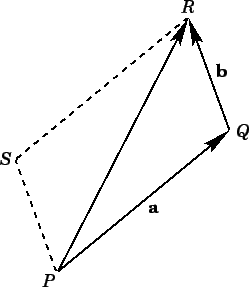
Figure 1:
 |
In applied mathematics, physical quantities are (predominately) represented by two distinct classes
of objects. Some quantities, denoted scalars, are represented by real
numbers. Others, denoted vectors, are represented by
directed line elements in space: e.g.,
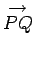 (see Fig. 1).
Note that line elements
(and, therefore, vectors) are movable, and do not carry intrinsic position information.
In fact, vectors just possess a magnitude and a direction, whereas scalars possess
a magnitude but no direction.
By convention, vector quantities are denoted by bold-faced characters (e.g.,
(see Fig. 1).
Note that line elements
(and, therefore, vectors) are movable, and do not carry intrinsic position information.
In fact, vectors just possess a magnitude and a direction, whereas scalars possess
a magnitude but no direction.
By convention, vector quantities are denoted by bold-faced characters (e.g.,
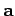 ) in
typeset documents, and by underlined characters
(e.g.,
) in
typeset documents, and by underlined characters
(e.g., 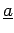 ) in long-hand.
Vectors can be added together, but the same units must be used, just like
in scalar addition. Vector addition
can be represented using a parallelogram:
) in long-hand.
Vectors can be added together, but the same units must be used, just like
in scalar addition. Vector addition
can be represented using a parallelogram:
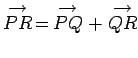 (see Fig. 2).
Suppose that
(see Fig. 2).
Suppose that
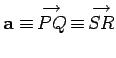 ,
,
 , and
, and
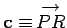 . It is clear
from Fig. 2 that vector addition is
commutative: i.e.,
. It is clear
from Fig. 2 that vector addition is
commutative: i.e.,
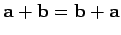 . It can also
be shown that the associative law holds: i.e.,
. It can also
be shown that the associative law holds: i.e.,
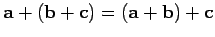 .
.
Figure 2:
 |
There are two approaches to vector analysis. The geometric approach is
based on line elements in space. The coordinate approach assumes that
space is defined by Cartesian coordinates, and uses these to characterize vectors.
In physics, we generally
adopt the second approach, because it is far more convenient.
In the coordinate approach, a vector is denoted as the row matrix of
its components along each of the Cartesian axes (the  -,
-,  -, and
-, and  -axes, say):
-axes, say):
 |
(1) |
Here, 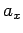 is the
is the  -coordinate of the ``head'' of the vector minus
the
-coordinate of the ``head'' of the vector minus
the  -coordinate of its ``tail.''
If
-coordinate of its ``tail.''
If
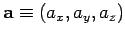 and
and
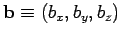 then vector addition is defined
then vector addition is defined
 |
(2) |
If 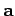 is a vector and
is a vector and 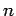 is a scalar then the product
of a scalar and a vector is defined
is a scalar then the product
of a scalar and a vector is defined
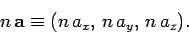 |
(3) |
It is clear that vector algebra is distributive with respect to
scalar multiplication: i.e.,
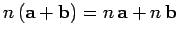 .
.
Unit vectors can be defined in the  -,
-,  -, and
-, and  -directions as
-directions as
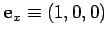 ,
,
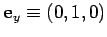 , and
, and
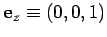 . Any vector can be written in terms of these unit vectors:
. Any vector can be written in terms of these unit vectors:
 |
(4) |
In mathematical terminology,
three vectors used in this manner form a basis of the vector space. If the
three vectors are mutually perpendicular then they are termed orthogonal basis
vectors. However, any set of three non-coplanar vectors can be used as basis
vectors.
Examples of vectors in physics are displacements from an origin,
 |
(5) |
and velocities,
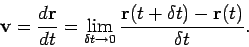 |
(6) |
Figure 3:
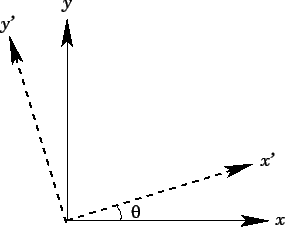 |
Suppose that we transform to a new orthogonal basis, the 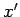 -,
-, 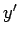 -, and
-, and  -axes,
which are related to the
-axes,
which are related to the  -,
-,  -, and
-, and  -axes via a rotation through an angle
-axes via a rotation through an angle
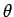 around the
around the  -axis (see Fig. 3).
In the new basis, the coordinates of the general displacement
-axis (see Fig. 3).
In the new basis, the coordinates of the general displacement 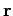 from the
origin are
from the
origin are 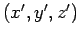 . These coordinates are related to the previous
coordinates via the transformation:
. These coordinates are related to the previous
coordinates via the transformation:
We do not need to change our notation for the displacement in the new basis.
It is still denoted 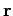 . The reason for this is that the magnitude and
direction of
. The reason for this is that the magnitude and
direction of 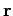 are independent of the choice of basis vectors. The
coordinates of
are independent of the choice of basis vectors. The
coordinates of 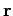 do depend on the choice of basis vectors.
However, they must depend in a very specific manner [i.e., Eqs. (7)-(9)] which
preserves the magnitude and direction of
do depend on the choice of basis vectors.
However, they must depend in a very specific manner [i.e., Eqs. (7)-(9)] which
preserves the magnitude and direction of 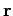 .
.
Since any vector can be represented as a displacement from an origin
(this is just a special case of a directed line element), it follows that
the
components of a general vector 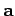 must transform in an analogous
manner to Eqs. (7)-(9). Thus,
must transform in an analogous
manner to Eqs. (7)-(9). Thus,
with similar transformation rules for rotation about the  - and
- and  -axes.
In the coordinate approach, Eqs. (10)-(12) constitute the definition of a vector.
The three
quantities (
-axes.
In the coordinate approach, Eqs. (10)-(12) constitute the definition of a vector.
The three
quantities (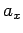 ,
, 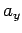 ,
, 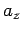 ) are the components of a vector provided that
they transform under rotation like Eqs. (10)-(12).
Conversely, (
) are the components of a vector provided that
they transform under rotation like Eqs. (10)-(12).
Conversely, (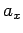 ,
, 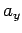 ,
, 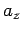 ) cannot be the components of a vector if they
do not transform like Eqs. (10)-(12). Scalar quantities are invariant
under transformation.
Thus, the individual components of a vector (
) cannot be the components of a vector if they
do not transform like Eqs. (10)-(12). Scalar quantities are invariant
under transformation.
Thus, the individual components of a vector (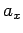 , say) are real numbers, but
they are
not scalars.
Displacement vectors, and all vectors derived from
displacements, automatically satisfy Eqs. (10)-(12). There are, however, other
physical quantities which have both magnitude and direction, but which are not
obviously related to displacements. We need to check carefully to see whether these
quantities are vectors.
, say) are real numbers, but
they are
not scalars.
Displacement vectors, and all vectors derived from
displacements, automatically satisfy Eqs. (10)-(12). There are, however, other
physical quantities which have both magnitude and direction, but which are not
obviously related to displacements. We need to check carefully to see whether these
quantities are vectors.



Next: Vector areas
Up: Vectors
Previous: Introduction
Richard Fitzpatrick
2006-02-02

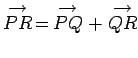 (see Fig. 2).
Suppose that
(see Fig. 2).
Suppose that
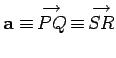 ,
,
 , and
, and
![]() -,
-, ![]() -, and
-, and ![]() -axes, say):
-axes, say):
![]() -,
-, ![]() -, and
-, and ![]() -directions as
-directions as
![]() ,
,
![]() , and
, and
![]() . Any vector can be written in terms of these unit vectors:
. Any vector can be written in terms of these unit vectors:
![]() must transform in an analogous
manner to Eqs. (7)-(9). Thus,
must transform in an analogous
manner to Eqs. (7)-(9). Thus,