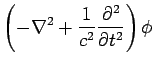Next: Gauge invariance
Up: Relativity and electromagnetism
Previous: The current density 4-vector
There are many ways of writing the laws of electromagnetism. However, the
most obviously Lorentz invariant way is to write them in terms of the
vector and scalar potentials (see Sect. 4.6). When written in this fashion, Maxwell's
equations reduce to
where  is the scalar potential, and
is the scalar potential, and  the vector potential.
Note that the differential operator appearing in these equations is
the Lorentz invariant d'Alembertian, defined in Eq. (1409).
Thus, the above pair
of equations can be rewritten in the form
the vector potential.
Note that the differential operator appearing in these equations is
the Lorentz invariant d'Alembertian, defined in Eq. (1409).
Thus, the above pair
of equations can be rewritten in the form
Maxwell's equations can be written in Lorentz invariant form provided that
the entity
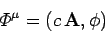 |
(1441) |
transforms as a contravariant 4-vector. This entity is known as the
potential 4-vector. It follows from Eqs. (1433), (1437), and (1438)
that
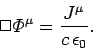 |
(1442) |
Thus, the field equations which govern classical electromagnetism can all
be summed up in a single 4-vector equation.



Next: Gauge invariance
Up: Relativity and electromagnetism
Previous: The current density 4-vector
Richard Fitzpatrick
2006-02-02