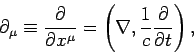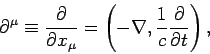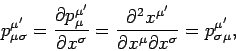Next: Proper time
Up: Relativity and electromagnetism
Previous: The physical significance of
Space-time
In special relativity, we are only allowed to use inertial frames to
assign coordinates to events. There are many different types of
inertial frames. However, it is convenient to adhere to those with
standard
coordinates. That is, spatial coordinates which are right-handed rectilinear
Cartesians based on a standard unit of length, and time-scales based on
a standard unit of time. We shall continue to assume that we are employing
standard coordinates. However, from now on, we shall make no assumptions
about the relative configuration of the
two sets of spatial axes, and the origins of time, when dealing with two
inertial frames. Thus, the most general transformation between two
inertial frames consists of a Lorentz transformation in the standard
configuration plus a translation (this includes a translation in time)
and a rotation of the coordinate axes. The resulting transformation is
called a general Lorentz transformation, as opposed to a Lorentz
transformation in the standard configuration, which will henceforth be termed
a standard Lorentz transformation.
In Sect. 10.3, we proved quite generally that corresponding differentials
in two inertial frames  and
and  satisfy the relation
satisfy the relation
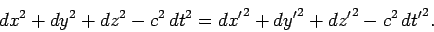 |
(1391) |
Thus, we expect this relation to remain invariant under a general Lorentz
transformation. Since such a transformation is linear, it follows that
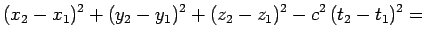 |
|
|
|
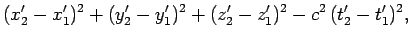 |
|
|
(1392) |
where
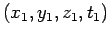 and
and
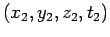 are the
coordinates of any two events in
are the
coordinates of any two events in  , and the primed symbols denote the
corresponding coordinates in
, and the primed symbols denote the
corresponding coordinates in 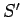 . It is convenient to write
. It is convenient to write
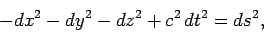 |
(1393) |
and
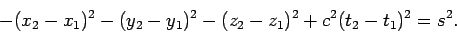 |
(1394) |
The differential 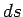 , or the finite number
, or the finite number 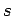 , defined by these
equations is called the interval between the corresponding events.
Equations (1393) and (1394) express the fact that the interval between
two events is invariant, in the sense that it has the same value in
all inertial frames. In other words, the interval between two
events is invariant under a general Lorentz transformation.
, defined by these
equations is called the interval between the corresponding events.
Equations (1393) and (1394) express the fact that the interval between
two events is invariant, in the sense that it has the same value in
all inertial frames. In other words, the interval between two
events is invariant under a general Lorentz transformation.
Let us consider entities defined in terms of four variables,
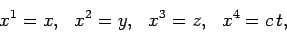 |
(1395) |
and which transform as tensors under a
general Lorentz transformation. From now on, such entities will be referred
to as 4-tensors.
Tensor analysis cannot proceed very far without the introduction of
a non-singular tensor 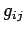 , the so-called fundamental tensor,
which is used to define the operations of raising and lowering
suffixes. The fundamental tensor is
usually introduced using a metric
, the so-called fundamental tensor,
which is used to define the operations of raising and lowering
suffixes. The fundamental tensor is
usually introduced using a metric
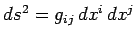 , where
, where
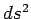 is a differential invariant. We have already come
across such an invariant, namely
is a differential invariant. We have already come
across such an invariant, namely
where 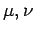 run from 1 to 4. Note that the use of Greek suffixes is
conventional in 4-tensor theory. Roman suffixes are reserved for
tensors in three-dimensional Euclidian space,
so-called 3-tensors. The 4-tensor
run from 1 to 4. Note that the use of Greek suffixes is
conventional in 4-tensor theory. Roman suffixes are reserved for
tensors in three-dimensional Euclidian space,
so-called 3-tensors. The 4-tensor 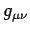 has the
components
has the
components
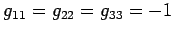 ,
, 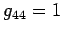 , and
, and 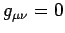 when
when
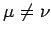 , in all permissible coordinate frames. From now on,
, in all permissible coordinate frames. From now on,
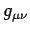 , as defined above, is adopted as the fundamental tensor
for 4-tensors.
, as defined above, is adopted as the fundamental tensor
for 4-tensors. 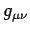 can be thought of as the metric
tensor of the space whose points are the events
can be thought of as the metric
tensor of the space whose points are the events
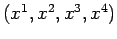 . This space is usually referred to as
space-time, for obvious reasons. Note that space-time cannot
be regarded as a straightforward generalization of Euclidian 3-space to
four dimensions, with time as the fourth dimension. The distribution
of signs in the metric ensures that the time coordinate
. This space is usually referred to as
space-time, for obvious reasons. Note that space-time cannot
be regarded as a straightforward generalization of Euclidian 3-space to
four dimensions, with time as the fourth dimension. The distribution
of signs in the metric ensures that the time coordinate 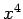 is not on
the same footing as the three space coordinates. Thus, space-time
has a non-isotropic nature which is quite unlike Euclidian
space, with its positive definite metric. According to the
relativity principle, all physical laws are expressible as interrelationships
between 4-tensors in space-time.
is not on
the same footing as the three space coordinates. Thus, space-time
has a non-isotropic nature which is quite unlike Euclidian
space, with its positive definite metric. According to the
relativity principle, all physical laws are expressible as interrelationships
between 4-tensors in space-time.
A tensor of rank one is called a 4-vector. We shall also have occasion
to use ordinary vectors in three-dimensional Euclidian space. Such
vectors are called 3-vectors, and are conventionally represented by
boldface symbols. We shall use the Latin suffixes 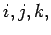 etc.,
to denote the components of a 3-vector: these suffixes are understood to
range from 1 to 3. Thus,
etc.,
to denote the components of a 3-vector: these suffixes are understood to
range from 1 to 3. Thus,
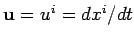 denotes a velocity
vector. For 3-vectors, we shall use the notation
denotes a velocity
vector. For 3-vectors, we shall use the notation
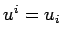 interchangeably: i.e., the level of the suffix has
no physical significance.
interchangeably: i.e., the level of the suffix has
no physical significance.
When tensor transformations from one frame to another actually
have to be computed, we shall usually find it possible to choose
coordinates in the standard configuration, so that the standard
Lorentz transform applies. Under such a transformation, any contravariant 4-vector,
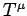 , transforms according to the same scheme as the difference
in coordinates
, transforms according to the same scheme as the difference
in coordinates
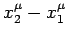 between two points in space-time.
It follows that
between two points in space-time.
It follows that
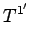 |
 |
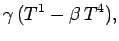 |
(1397) |
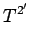 |
 |
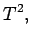 |
(1398) |
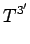 |
 |
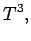 |
(1399) |
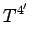 |
 |
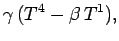 |
(1400) |
where 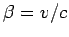 . Higher rank 4-tensors transform according to
the rules (1372)-(1374). The transformation coefficients take the form
. Higher rank 4-tensors transform according to
the rules (1372)-(1374). The transformation coefficients take the form
Often the first three components of a 4-vector coincide with the
components of a 3-vector. For example, the 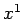 ,
, 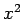 ,
, 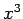 in
in
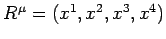 are the components of
are the components of 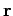 , the position
3-vector of the point at which the event occurs. In such cases, we
adopt the notation exemplified by
, the position
3-vector of the point at which the event occurs. In such cases, we
adopt the notation exemplified by
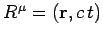 . The covariant
form of such a vector is simply
. The covariant
form of such a vector is simply
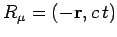 . The squared
magnitude of the vector is
. The squared
magnitude of the vector is
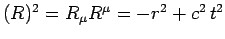 .
The inner product
.
The inner product
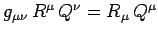 of
of
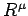 with a similar vector
with a similar vector
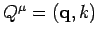 is given by
is given by
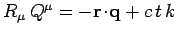 . The vectors
. The vectors
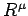 and
and 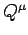 are said to be orthogonal if
are said to be orthogonal if
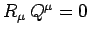 .
.
Since a general Lorentz transformation is a linear transformation,
the partial derivative of a 4-tensor is also a 4-tensor:
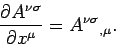 |
(1403) |
Clearly, a general 4-tensor acquires an extra covariant index after
partial differentiation with respect to the contravariant
coordinate 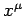 . It is helpful to define a covariant derivative operator
. It is helpful to define a covariant derivative operator
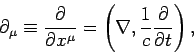 |
(1404) |
where
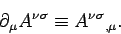 |
(1405) |
There is a corresponding contravariant derivative operator
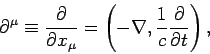 |
(1406) |
where
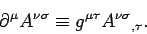 |
(1407) |
The 4-divergence of a 4-vector,
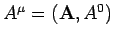 , is the invariant
, is the invariant
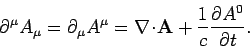 |
(1408) |
The four-dimensional Laplacian operator, or d'Alembertian,
is equivalent to the invariant contraction
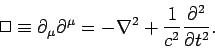 |
(1409) |
Recall that we still need to prove (from Sect. 10.3) that the invariance
of the differential metric,
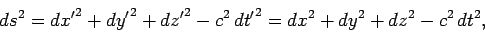 |
(1410) |
between two general inertial frames implies that the coordinate transformation
between
such frames is necessarily linear. To put it another way, we need to
demonstrate that a transformation which transforms a metric
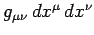 with constant coefficients into a metric
with constant coefficients into a metric
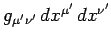 with constant coefficients must be linear.
Now
with constant coefficients must be linear.
Now
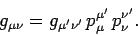 |
(1411) |
Differentiating with respect to 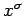 , we get
, we get
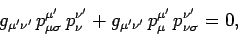 |
(1412) |
where
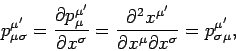 |
(1413) |
etc.
Interchanging the indices 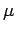 and
and 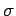 yields
yields
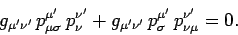 |
(1414) |
Interchanging the indices 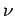 and
and 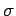 gives
gives
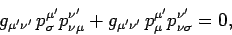 |
(1415) |
where the indices 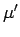 and
and 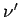 have been interchanged in the first term.
It follows from Eqs. (1412), (1414), and (1415) that
have been interchanged in the first term.
It follows from Eqs. (1412), (1414), and (1415) that
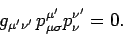 |
(1416) |
Multiplication by
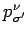 yields
yields
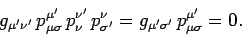 |
(1417) |
Finally, multiplication by
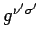 gives
gives
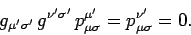 |
(1418) |
This proves that the coefficients
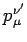 are constants, and, hence,
that the transformation is linear.
are constants, and, hence,
that the transformation is linear.



Next: Proper time
Up: Relativity and electromagnetism
Previous: The physical significance of
Richard Fitzpatrick
2006-02-02
![]() and
and ![]() satisfy the relation
satisfy the relation
![]() , the so-called fundamental tensor,
which is used to define the operations of raising and lowering
suffixes. The fundamental tensor is
usually introduced using a metric
, the so-called fundamental tensor,
which is used to define the operations of raising and lowering
suffixes. The fundamental tensor is
usually introduced using a metric
![]() , where
, where
![]() is a differential invariant. We have already come
across such an invariant, namely
is a differential invariant. We have already come
across such an invariant, namely
![]() etc.,
to denote the components of a 3-vector: these suffixes are understood to
range from 1 to 3. Thus,
etc.,
to denote the components of a 3-vector: these suffixes are understood to
range from 1 to 3. Thus,
![]() denotes a velocity
vector. For 3-vectors, we shall use the notation
denotes a velocity
vector. For 3-vectors, we shall use the notation
![]() interchangeably: i.e., the level of the suffix has
no physical significance.
interchangeably: i.e., the level of the suffix has
no physical significance.
![]() , transforms according to the same scheme as the difference
in coordinates
, transforms according to the same scheme as the difference
in coordinates
![]() between two points in space-time.
It follows that
between two points in space-time.
It follows that
![]() ,
, ![]() ,
, ![]() in
in
![]() are the components of
are the components of ![]() , the position
3-vector of the point at which the event occurs. In such cases, we
adopt the notation exemplified by
, the position
3-vector of the point at which the event occurs. In such cases, we
adopt the notation exemplified by
![]() . The covariant
form of such a vector is simply
. The covariant
form of such a vector is simply
![]() . The squared
magnitude of the vector is
. The squared
magnitude of the vector is
![]() .
The inner product
.
The inner product
![]() of
of
![]() with a similar vector
with a similar vector
![]() is given by
is given by
![]() . The vectors
. The vectors
![]() and
and ![]() are said to be orthogonal if
are said to be orthogonal if
![]() .
.