Next: Elliptic orbits Up: Keplerian orbits Previous: Orbital energies
 , and Equations (4.41) and (4.44)
can be combined to give
Here,
, and Equations (4.41) and (4.44)
can be combined to give
Here,
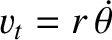 is the satellite's tangential velocity, and
is the satellite's tangential velocity, and
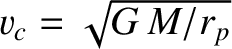 is the tangential velocity that it would need to
maintain a circular orbit at the perihelion distance.
Likewise, at aphelion,
where
is the tangential velocity that it would need to
maintain a circular orbit at the perihelion distance.
Likewise, at aphelion,
where
 is now the tangential velocity that the
satellite would need to maintain a circular orbit at the aphelion distance.
is now the tangential velocity that the
satellite would need to maintain a circular orbit at the aphelion distance.
Suppose that our satellite is initially in a circular orbit of radius  , and that we wish
to transfer it into a circular orbit of radius
, and that we wish
to transfer it into a circular orbit of radius 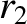 , where
, where  . We can
achieve this by temporarily placing the satellite in an elliptical orbit
whose perihelion distance is
. We can
achieve this by temporarily placing the satellite in an elliptical orbit
whose perihelion distance is  , and whose aphelion distance is
, and whose aphelion distance is 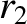 .
It follows, from Equation (4.37), that the required eccentricity of the elliptical
orbit is
.
It follows, from Equation (4.37), that the required eccentricity of the elliptical
orbit is
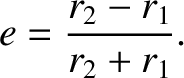 |
(4.48) |
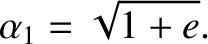 |
(4.49) |
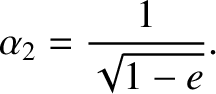 |
(4.50) |
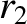 .
This process is illustrated in Figure 4.4. Obviously, we can transfer
our satellite from a larger to a smaller circular orbit by performing
the preceding process in reverse. Note, finally, from Equation (4.46), that if we
increase the tangential velocity of a satellite in a circular orbit about the Sun by a
factor greater than
.
This process is illustrated in Figure 4.4. Obviously, we can transfer
our satellite from a larger to a smaller circular orbit by performing
the preceding process in reverse. Note, finally, from Equation (4.46), that if we
increase the tangential velocity of a satellite in a circular orbit about the Sun by a
factor greater than 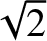 then we will transfer it into a
hyperbolic orbit (
then we will transfer it into a
hyperbolic orbit (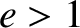 ), and it will eventually escape from the Sun's
gravitational field.
), and it will eventually escape from the Sun's
gravitational field.