Next: Evection Up: Lunar motion Previous: Annual equation
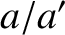 .
.
According to Equations (11.138) and (11.150),
where we have neglected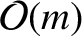 contributions.
It follows from Equations (11.192), (11.193), and (11.204) that
contributions.
It follows from Equations (11.192), (11.193), and (11.204) that
 |
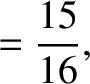 |
(11.248) |
 |
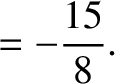 |
(11.249) |
 , Equations (11.138) and (11.150) give
, Equations (11.138) and (11.150) give
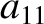 |
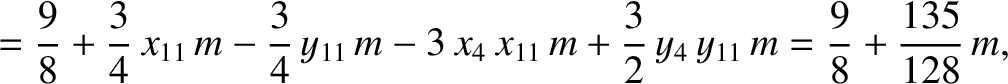 |
(11.250) |
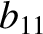 |
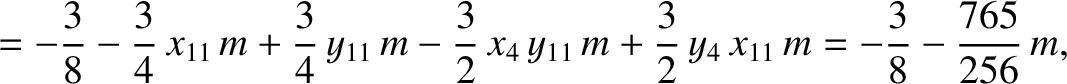 |
(11.251) |
 and
and 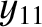 .
Hence, Equations (11.192), (11.193), and (11.204) yield
.
Hence, Equations (11.192), (11.193), and (11.204) yield
According to Equations (11.139) and (11.151),
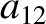 |
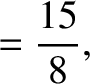 |
(11.254) |
 |
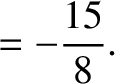 |
(11.255) |
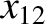 |
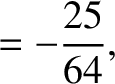 |
(11.256) |
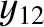 |
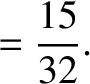 |
(11.257) |
It follows from Equations (11.76), (11.122)–(11.124), (11.170), (11.171), (11.182), and (11.183), as well as the previous expressions for  ,
, 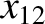 ,
, 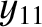 , and
, and 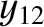 , that the net perturbation to the lunar orbit
due to terms in the solution of the lunar equations of motion that depend linearly on
, that the net perturbation to the lunar orbit
due to terms in the solution of the lunar equations of motion that depend linearly on 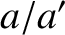 is
is
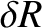 |
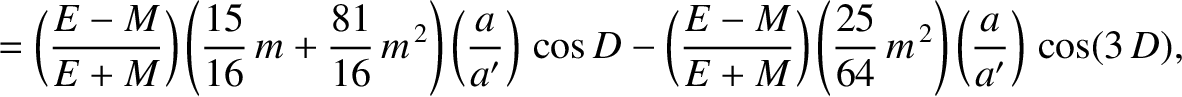 |
(11.258) |
 |
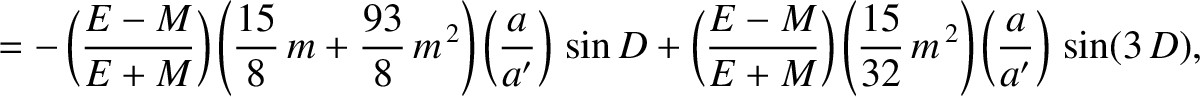 |
(11.259) |
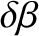 |
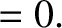 |
(11.260) |
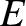 is the mass of the Earth, and
is the mass of the Earth, and  the mass of the moon.
The previous expressions are accurate to
the mass of the moon.
The previous expressions are accurate to
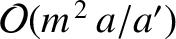 .
.
The first term on the right-hand side of Equation (11.259) is known as the parallactic inequality. The parallactic inequality attains its maximum amplitude when the Moon in half illuminated (i.e., when
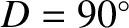 or
or
 ). Conversely, the amplitude of the parallactic inequality is zero when the Moon is either fully illuminated or not illuminated at all (i.e., when
). Conversely, the amplitude of the parallactic inequality is zero when the Moon is either fully illuminated or not illuminated at all (i.e., when
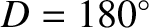 or
or 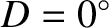 ).
According to Equation (11.259), the parallactic inequality generates a perturbation in the lunar ecliptic longitude that oscillates with a period
of a synodic month, and has an amplitude (calculated using
).
According to Equation (11.259), the parallactic inequality generates a perturbation in the lunar ecliptic longitude that oscillates with a period
of a synodic month, and has an amplitude (calculated using 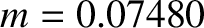 ,
,
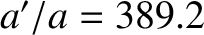 , and
, and 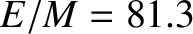 ) of
) of 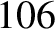 arc seconds (Yoder 1995). As before, the oscillation period is in good agreement with
observations, whereas the amplitude is somewhat inaccurate [it should be
arc seconds (Yoder 1995). As before, the oscillation period is in good agreement with
observations, whereas the amplitude is somewhat inaccurate [it should be 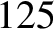 arc seconds (Chapront-Touzé and Chapront 1988)] because of the
omission of higher-order (in
arc seconds (Chapront-Touzé and Chapront 1988)] because of the
omission of higher-order (in  ) contributions.
) contributions.