Next: Useful definitions Up: Lunar motion Previous: Solar orbit
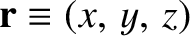 . It is helpful to define
as well as
Here,
. It is helpful to define
as well as
Here, 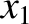 ,
, 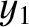 ,
, 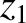 and
and 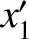 ,
, 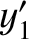 ,
, 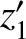 are the Cartesian coordinates of the Moon (relative to the Earth) and the
Sun (relative to the Earth–Moon barycenter), respectively, in a reference frame that rotates at angular velocity
are the Cartesian coordinates of the Moon (relative to the Earth) and the
Sun (relative to the Earth–Moon barycenter), respectively, in a reference frame that rotates at angular velocity 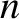 (i.e., the Moon's
mean orbital angular velocity) about an axis perpendicular to the ecliptic plane.
Note that if the lunar orbit were a circle, centered on the Earth, and lying in the ecliptic plane, then the coordinates
(i.e., the Moon's
mean orbital angular velocity) about an axis perpendicular to the ecliptic plane.
Note that if the lunar orbit were a circle, centered on the Earth, and lying in the ecliptic plane, then the coordinates 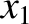 ,
, 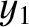 , and
, and 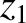 would all be
independent of time. In fact, the small eccentricity of the lunar orbit,
would all be
independent of time. In fact, the small eccentricity of the lunar orbit, 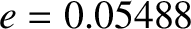 , combined with its slight inclination to the
ecliptic plane,
, combined with its slight inclination to the
ecliptic plane,
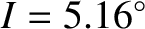 , as well as the various solar perturbations, generate small-amplitude oscillations in
, as well as the various solar perturbations, generate small-amplitude oscillations in 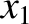 ,
, 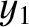 , and
, and 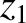 (Yoder 1995).
(Yoder 1995).
Equations (11.41)–(11.43) and (11.47)–(11.49) yield
It is also easily demonstrated thatThe Cartesian components of the lunar equation of motion, (11.33), are
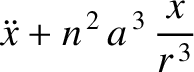 |
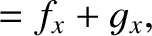 |
(11.54) |
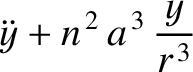 |
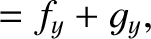 |
(11.55) |
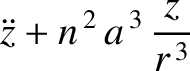 |
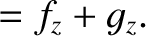 |
(11.56) |
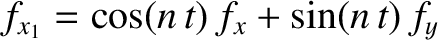 ,
,
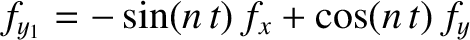 ,
,
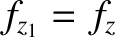 , et cetera.
, et cetera.
It is convenient, at this stage, to adopt the following normalization scheme:
with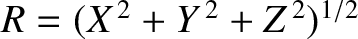 ,
,
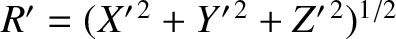 , and
, and 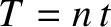 .
In normalized form, Equation (11.50)–(11.53) become
whereas
Equations (11.57)–(11.59) yield
Here,
where
.
In normalized form, Equation (11.50)–(11.53) become
whereas
Equations (11.57)–(11.59) yield
Here,
where
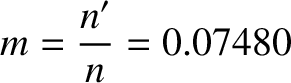 |
(11.75) |
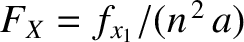 ,
,
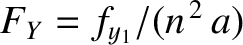 , et cetera. Finally,
, et cetera. Finally,
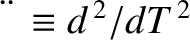 and
and
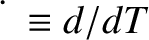 .
.
Equations (11.62)–(11.65) and (11.69)–(11.71) yield
Likewise, (11.62)–(11.65) and (11.72)–(11.74) give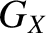 |
![$\displaystyle \simeq m^{\,2}\,\zeta \left\{\left(\frac{9}{8}\,\cos[(1-m)\,T]+\frac{15}{8}\,\cos[3\,(1-m)\,T]\right)X^{\,2}\right.$](img3126.png) |
|
![$\displaystyle \phantom{=} + \left(\frac{3}{8}\,\cos[(1-m)\,T]-\frac{15}{8}\,\cos[3\,(1-m)\,T]\right)Y^{\,2}$](img3127.png) |
||
![$\displaystyle \phantom{=} \left.- \left(\frac{3}{4}\,\sin[(1-m)\,T]+\frac{15}{4...
...,(1-m)\,T]\right)X\,Y -\left(\frac{3}{2}\,\cos[(1-m)\,T]\right)Z^{\,2}\right\},$](img3128.png) |
(11.80) | |
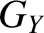 |
![$\displaystyle \simeq m^{\,2}\,\zeta \left\{-\left(\frac{3}{8}\,\sin[(1-m)\,T]+\frac{15}{8}\,\sin[3\,(1-m)\,T]\right)X^{\,2}\right.$](img3129.png) |
|
![$\displaystyle \phantom{=} + \left(-\frac{9}{8}\,\sin[(1-m)\,T]+\frac{15}{8}\,\sin[3\,(1-m)\,T]\right)Y^{\,2}$](img3130.png) |
||
![$\displaystyle \phantom{=} \left.+ \left(\frac{3}{4}\,\cos[(1-m)\,T]-\frac{15}{4...
...,(1-m)\,T]\right)X\,Y +\left(\frac{3}{2}\,\sin[(1-m)\,T]\right)Z^{\,2}\right\},$](img3131.png) |
(11.81) | |
 |
![$\displaystyle \simeq m^{\,2}\,\zeta \left(-3\,\cos[(1-m)\,T]\,X\,Z + 3\,\sin[(1-m)\,T]\, Y\,Z \right).$](img3132.png) |
(11.82) |
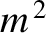 ,
, 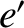 , and
, and 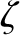 .
.
Finally, let us write
Here,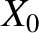 is a constant, and
is a constant, and
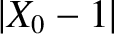 ,
,
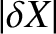 ,
,
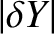 ,
,
 .
Expanding Equations (11.66)–(11.68) and (11.77)–(11.82), and neglecting terms that are third order, or greater, in the small parameters
.
Expanding Equations (11.66)–(11.68) and (11.77)–(11.82), and neglecting terms that are third order, or greater, in the small parameters 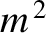 ,
,
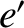 ,
, 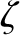 ,
, 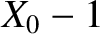 ,
, 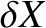 ,
, 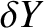 , and
, and
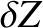 , we obtain
where
, we obtain
where
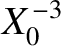 |
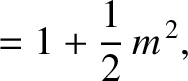 |
(11.89) |
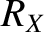 |
![$\displaystyle \simeq
\frac{3}{2}\,m^{\,2}\,X_0\,\cos[2\,(1-m)\,T]$](img3155.png) |
|
![$\displaystyle \phantom{=} +\frac{3}{2}\,m^{\,2}\,e'\,\cos(m\,T) + \frac{21}{4}\,m^{\,2}\,e'\,\cos[(2-3\,m)\,T]-\frac{3}{4}\,m^{\,2}\,e'\,\cos[(2-m)\,T]$](img3156.png) |
||
![$\displaystyle \phantom{=} +\frac{9}{8}\,m^{\,2}\,\zeta\,\cos[(1-m)\,T] + \frac{15}{8}\,m^{\,2}\,\zeta\,\cos[3\,(1-m)\,T]$](img3157.png) |
||
![$\displaystyle \phantom{=}+ \frac{3}{2}\,m^{\,2}\,\cos[2\,(1-m)\,T]\,\delta X -\frac{3}{2}\,m^{\,2}\,\sin[2\,(1-m)\,T]\,\delta Y$](img3158.png) |
||
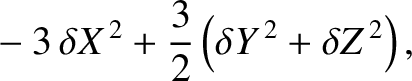 |
(11.90) | |
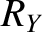 |
![$\displaystyle \simeq -\frac{3}{2}\,m^{\,2}\,X_0\,\sin[2\,(1-m)\,T]$](img3161.png) |
|
![$\displaystyle \phantom{=} - \frac{21}{4}\,m^{\,2}\,e'\,\sin[(2-3\,m)\,T]+\frac{3}{4}\,m^{\,2}\,e'\,\sin[(2-m)\,T]$](img3162.png) |
||
![$\displaystyle \phantom{=} -\frac{3}{8}\,m^{\,2}\,\zeta\,\sin[(1-m)\,T] - \frac{15}{8}\,m^{\,2}\,\zeta\,\sin[3\,(1-m)\,T],$](img3163.png) |
(11.91) | |
![$\displaystyle \phantom{=}-\frac{3}{2}\,m^{\,2}\,\sin[2\,(1-m)\,T]\,\delta X -\frac{3}{2}\,m^{\,2}\,\cos[2\,(1-m)\,T]\,\delta Y+3\,\delta X\,\delta Y,$](img3164.png) |
(11.92) | |
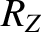 |
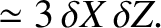 |
(11.93) |
After Equations (11.86)–(11.93) have been solved for 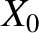 ,
, 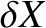 ,
, 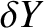 , and
, and 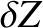 , the geocentric Cartesian coordinates, (
, the geocentric Cartesian coordinates, ( ,
,  ,
,  ), of the Moon in the
non-rotating reference
frame are obtained from Equations (11.44)–(11.46), (11.60)–(11.61), and (11.83)–(11.85). However, it is more convenient to write
), of the Moon in the
non-rotating reference
frame are obtained from Equations (11.44)–(11.46), (11.60)–(11.61), and (11.83)–(11.85). However, it is more convenient to write
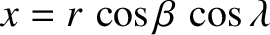 ,
,
 , and
, and
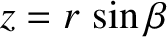 , where
, where  is the radial distance between the Earth and Moon, and
is the radial distance between the Earth and Moon, and 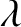 and
and 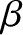 are termed the Moon's geocentric (i.e., centered on the Earth) ecliptic
longitude and ecliptic latitude, respectively. Moreover, it is easily seen that, neglecting terms that are third order, or greater, in the small parameters
are termed the Moon's geocentric (i.e., centered on the Earth) ecliptic
longitude and ecliptic latitude, respectively. Moreover, it is easily seen that, neglecting terms that are third order, or greater, in the small parameters 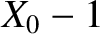 ,
, 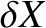 ,
, 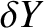 , and
, and 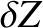 ,
,