Next: Zero-velocity surfaces Up: Three-body problem Previous: Co-rotating frame
 in the rotating reference frame. Such points
are termed Lagrange points. Hence, in the rotating frame, the mass
in the rotating reference frame. Such points
are termed Lagrange points. Hence, in the rotating frame, the mass  would remain at rest if placed at one of the Lagrange points. It is, thus, clear that these points are
fixed in the rotating frame.
Conversely, in the inertial reference frame, the Lagrange points rotate about the center of mass with
angular velocity
would remain at rest if placed at one of the Lagrange points. It is, thus, clear that these points are
fixed in the rotating frame.
Conversely, in the inertial reference frame, the Lagrange points rotate about the center of mass with
angular velocity  , and the mass
, and the mass  would consequently also rotate about the center
of mass with angular velocity
would consequently also rotate about the center
of mass with angular velocity  if placed at one of these points (with the appropriate
velocity). In the following,
we shall assume, without loss of generality, that
if placed at one of these points (with the appropriate
velocity). In the following,
we shall assume, without loss of generality, that
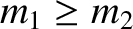 .
.
The Lagrange points satisfy
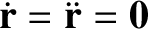 in the rotating frame.
It thus follows, from Equations (9.27)–(9.29), that the Lagrange
points are the solutions of
in the rotating frame.
It thus follows, from Equations (9.27)–(9.29), that the Lagrange
points are the solutions of
 |
(9.37) |
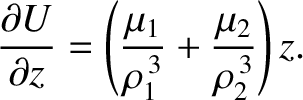 |
(9.38) |
 . Hence, all of the Lagrange points lie in the
. Hence, all of the Lagrange points lie in the  -
- plane.
plane.
If  , it is readily demonstrated that
, it is readily demonstrated that
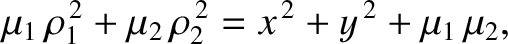 |
(9.39) |
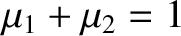 .
Hence, Equation (9.30) can also be written
The Lagrange points thus satisfy
which reduce to
.
Hence, Equation (9.30) can also be written
The Lagrange points thus satisfy
which reduce to
One obvious solution of Equation (9.44) is  , corresponding to a Lagrange
point that lies on the
, corresponding to a Lagrange
point that lies on the  -axis. It turns out that there are three such points:
-axis. It turns out that there are three such points: 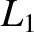 lies between masses
lies between masses  and
and 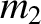 ,
, 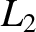 lies to the right of mass
lies to the right of mass 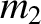 , and
, and
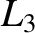 lies to the left of mass
lies to the left of mass  . See Figure 9.6. At the
. See Figure 9.6. At the 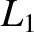 point,
we have
point,
we have
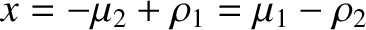 and
and
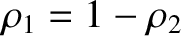 . Hence, from Equation (9.43),
. Hence, from Equation (9.43),
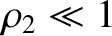 , we can find an approximate solution of Equation (9.45)
by expanding in powers of
, we can find an approximate solution of Equation (9.45)
by expanding in powers of  :
This equation can be inverted to give
where
:
This equation can be inverted to give
where
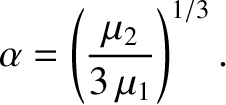 |
(9.48) |
At the 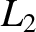 point,
we have
point,
we have
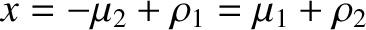 and
and
 .
Hence, from Equation (9.43),
.
Hence, from Equation (9.43),
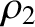 , we obtain
, we obtain
Finally, at the 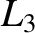 point,
we have
point,
we have
 and
and
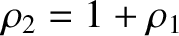 . Hence, from Equation (9.43),
. Hence, from Equation (9.43),
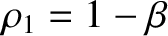 . Expanding in powers of
. Expanding in powers of 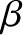 , we obtain
where
, we obtain
where
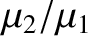 is assumed to be a small parameter.
is assumed to be a small parameter.
Let us now search for Lagrange points that do not lie on the  -axis. One obvious solution of Equations (9.41)
and (9.42) is
-axis. One obvious solution of Equations (9.41)
and (9.42) is
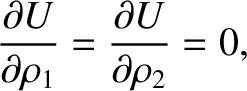 |
(9.55) |
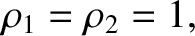 |
(9.56) |
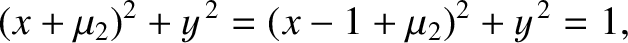 |
(9.57) |
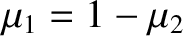 .
The two solutions of this equation are
.
The two solutions of this equation are
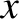 |
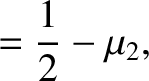 |
(9.58) |
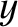 |
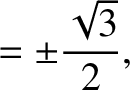 |
(9.59) |
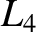 and
and  . Note that the point
. Note that the point 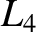 and the masses
and the masses
 and
and 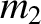 lie at the apexes of an equilateral triangle. The same is
true for the point
lie at the apexes of an equilateral triangle. The same is
true for the point  . We have now found all of the possible Lagrange points.
. We have now found all of the possible Lagrange points.
Figure 9.6 shows the positions of the two masses,  and
and 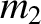 , and
the five Lagrange points,
, and
the five Lagrange points, 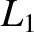 to
to  , calculated for the case where
, calculated for the case where 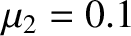 .
.