Next: Plane polar coordinates Up: Keplerian orbits Previous: Kepler's laws
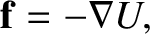 |
(4.3) |
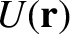 , of our planet in the Sun's gravitational field takes the form
(See Section 3.5.)
It follows that the total energy of our planet is a conserved quantity. (See Section 2.4.) In other words,
is constant in time. Here,
, of our planet in the Sun's gravitational field takes the form
(See Section 3.5.)
It follows that the total energy of our planet is a conserved quantity. (See Section 2.4.) In other words,
is constant in time. Here,  is actually the planet's total energy per unit
mass, and
is actually the planet's total energy per unit
mass, and
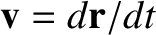 .
.
Gravity is also a central force. Hence, the angular momentum of our planet is a conserved quantity. (See Section 2.5.) In other words,
which is actually the planet's angular momentum per unit mass, is constant in time. Assuming that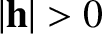 , and taking the scalar product of the preceding equation with
, and taking the scalar product of the preceding equation with  , we
obtain
, we
obtain
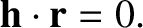 |
(4.7) |
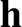 . Because
. Because 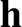 is a constant vector,
it always points in the same direction. We, therefore, conclude that
the orbit of our planet is two-dimensional; that is, it is confined to some fixed plane that passes through the origin. Without loss of generality, we can let this plane coincide with the
is a constant vector,
it always points in the same direction. We, therefore, conclude that
the orbit of our planet is two-dimensional; that is, it is confined to some fixed plane that passes through the origin. Without loss of generality, we can let this plane coincide with the  -
- plane.
plane.