Next: Kepler's laws Up: Keplerian orbits Previous: Keplerian orbits
 ,
is located at the origin of our coordinate system. Consider the motion of a general planet, of mass
,
is located at the origin of our coordinate system. Consider the motion of a general planet, of mass 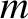 , that is located
at position vector
, that is located
at position vector 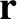 . Given that the Sun and all of the planets are approximately spherical, the gravitational force exerted on our
planet by the Sun can be written (see Chapter 3)
An equal and opposite force to that given in Equation (4.1) acts on the Sun. However, in this chapter, we shall assume that
the Sun is so much more massive than the planet that this force does not
cause the Sun's position to shift appreciably. Hence, the Sun will always remain
at the origin of our coordinate system. Likewise, we shall neglect the
gravitational forces exerted on our chosen planet by the other bodies in the solar system, compared to the gravitational
force exerted on it by the Sun. This is reasonable because the Sun is much more massive (by a factor of, at least,
. Given that the Sun and all of the planets are approximately spherical, the gravitational force exerted on our
planet by the Sun can be written (see Chapter 3)
An equal and opposite force to that given in Equation (4.1) acts on the Sun. However, in this chapter, we shall assume that
the Sun is so much more massive than the planet that this force does not
cause the Sun's position to shift appreciably. Hence, the Sun will always remain
at the origin of our coordinate system. Likewise, we shall neglect the
gravitational forces exerted on our chosen planet by the other bodies in the solar system, compared to the gravitational
force exerted on it by the Sun. This is reasonable because the Sun is much more massive (by a factor of, at least, 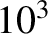 ) than any
other solar system body.
Thus, according to Equation (4.1) and Newton's second law of motion, the equation
of motion of our planet (which can effectively be treated as a point object; see Chapter 3) takes the form
Note that the planet's mass,
) than any
other solar system body.
Thus, according to Equation (4.1) and Newton's second law of motion, the equation
of motion of our planet (which can effectively be treated as a point object; see Chapter 3) takes the form
Note that the planet's mass, 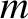 , has canceled out on both sides of
this equation.
, has canceled out on both sides of
this equation.