According to Equations (B.23), (B.38), and (B.39), Mercury's instantaneous perihelion precession rate, due to
the perturbing influence of some other planet in the solar system, takes the form
![$\displaystyle \dot{\varpi} =\frac{m'}{M+m}\,r^{\,2}\,r'\,\frac{\skew{5}\dot{\th...
...ta\,\beta\right]\left(\frac{1}{\delta^{\,3}}-\frac{1}{r'^{\,3}}\right)\right\},$](img4191.png) |
(B.39) |
where
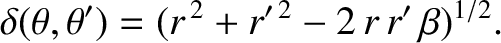 |
(B.40) |
However, we are only interested in the secular precession rate; that is, the mean rate over some timescale that is
much longer than either the orbital period of Mercury or that of the perturbing planet. We can obtain a formula for the
secular precession rate by averaging the previous expression over the orbits of the two planets. In other words,
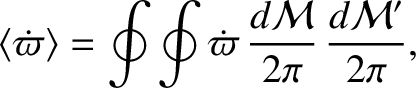 |
(B.41) |
where 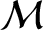 and
and 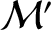 are the mean anomalies of Mercury and the perturbing planet, respectively. (See Section 4.11.)
Note that we must average in terms of the mean anomalies, rather than the true anomalies, because the former increase uniformly in time (unlike the latter).
In fact,
are the mean anomalies of Mercury and the perturbing planet, respectively. (See Section 4.11.)
Note that we must average in terms of the mean anomalies, rather than the true anomalies, because the former increase uniformly in time (unlike the latter).
In fact,
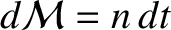 and
and
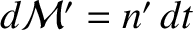 , where
, where  and
and 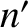 are the mean orbital angular velocities of
Mercury and the perturbing planet, respectively. (See Section 4.11.) Furthermore,
are the mean orbital angular velocities of
Mercury and the perturbing planet, respectively. (See Section 4.11.) Furthermore,
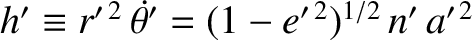 is a constant of the perturbing planet's motion. (See Section 4.8.)
Hence,
is a constant of the perturbing planet's motion. (See Section 4.8.)
Hence,
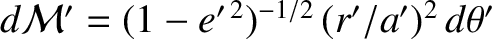 .
Thus, we obtain
where
.
Thus, we obtain
where 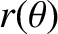 ,
,
 ,
,
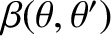 ,
,
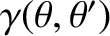 , and
, and
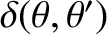 are specified in Equations (B.31), (B.32), (B.35), (B.36), and (B.41) respectively. Here,
are specified in Equations (B.31), (B.32), (B.35), (B.36), and (B.41) respectively. Here,
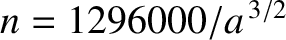 arc seconds per year (where
arc seconds per year (where  is measured in astronomical units).
The previous expression can be simplified somewhat, because some terms are obviously annihilated by the integration in
is measured in astronomical units).
The previous expression can be simplified somewhat, because some terms are obviously annihilated by the integration in 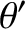 . In fact,
. In fact,
Table B.1:
Contributions to the secular precession rate of Mercury's perihelion from the other planets in the solar system.
| |
|
| Planet |
 |
| |
|
| Venus |
2.7745 |
| Earth |
0.9084 |
| Mars |
0.0248 |
| Jupiter |
1.5400 |
| Saturn |
0.0731 |
| Uranus |
0.0014 |
| Neptune |
0.0004 |
| Total |
5.3226 |
|
Table B.1 shows the contributions to the secular precession rate of Mercury's perihelion, due to the perturbing influence of the other planets in the solar system, calculated from
Equation (B.44), using the planetary mass and orbital element data given in Table 4.1. It can be seen that the dominant contributions
to the precession rate come from Venus, Earth, and Jupiter. Furthermore, the total precession rate is 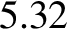 arc seconds per year.
arc seconds per year.
![$\displaystyle \dot{\varpi} =\frac{m'}{M+m}\,r^{\,2}\,r'\,\frac{\skew{5}\dot{\th...
...ta\,\beta\right]\left(\frac{1}{\delta^{\,3}}-\frac{1}{r'^{\,3}}\right)\right\},$](img4191.png)
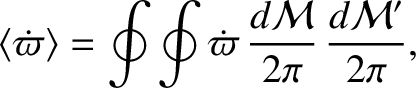
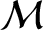 and
and 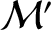 are the mean anomalies of Mercury and the perturbing planet, respectively. (See Section 4.11.)
Note that we must average in terms of the mean anomalies, rather than the true anomalies, because the former increase uniformly in time (unlike the latter).
In fact,
are the mean anomalies of Mercury and the perturbing planet, respectively. (See Section 4.11.)
Note that we must average in terms of the mean anomalies, rather than the true anomalies, because the former increase uniformly in time (unlike the latter).
In fact,
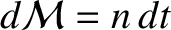 and
and
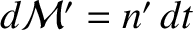 , where
, where  and
and 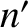 are the mean orbital angular velocities of
Mercury and the perturbing planet, respectively. (See Section 4.11.) Furthermore,
are the mean orbital angular velocities of
Mercury and the perturbing planet, respectively. (See Section 4.11.) Furthermore,
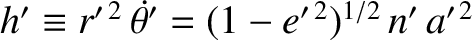 is a constant of the perturbing planet's motion. (See Section 4.8.)
Hence,
is a constant of the perturbing planet's motion. (See Section 4.8.)
Hence,
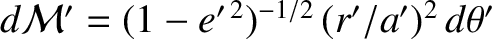 .
Thus, we obtain
.
Thus, we obtain
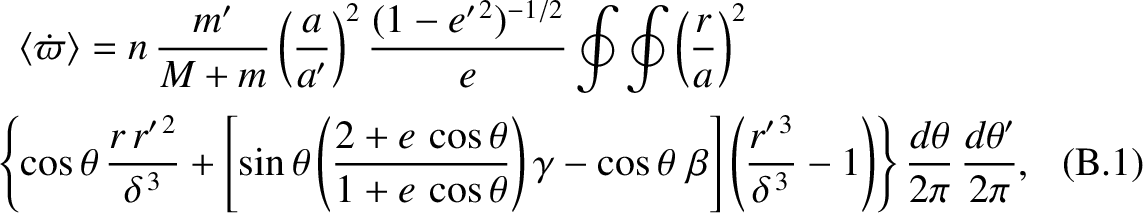
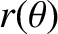 ,
,
 ,
,
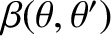 ,
,
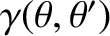 , and
, and
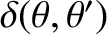 are specified in Equations (B.31), (B.32), (B.35), (B.36), and (B.41) respectively. Here,
are specified in Equations (B.31), (B.32), (B.35), (B.36), and (B.41) respectively. Here,
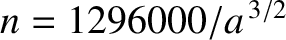 arc seconds per year (where
arc seconds per year (where  is measured in astronomical units).
The previous expression can be simplified somewhat, because some terms are obviously annihilated by the integration in
is measured in astronomical units).
The previous expression can be simplified somewhat, because some terms are obviously annihilated by the integration in 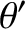 . In fact,
. In fact,
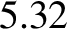 arc seconds per year.
arc seconds per year.