Elliptic orbits
Let us determine
the radial and angular coordinates,  and
and  , respectively, of
a planet in an elliptical orbit about the Sun as a function of time.
Suppose that the planet
passes through its perihelion point,
, respectively, of
a planet in an elliptical orbit about the Sun as a function of time.
Suppose that the planet
passes through its perihelion point, 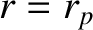 and
and 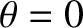 , at
, at 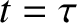 .
The constant
.
The constant 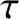 is termed the time of perihelion passage. It
follows from the previous analysis that
is termed the time of perihelion passage. It
follows from the previous analysis that
 |
(4.51) |
and
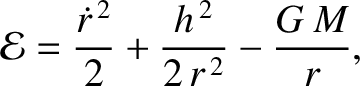 |
(4.52) |
where  ,
,
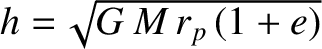 , and
, and
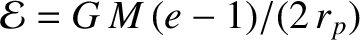 are the orbital eccentricity, angular momentum per unit mass, and
energy per unit mass, respectively. The preceding equation can be rearranged to
give
are the orbital eccentricity, angular momentum per unit mass, and
energy per unit mass, respectively. The preceding equation can be rearranged to
give
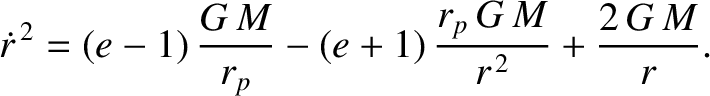 |
(4.53) |
Taking the square root, and integrating, we obtain
![$\displaystyle \int_{r_p}^r\frac{r\,dr}{[2\,r + (e-1)\,r^{\,2}/r_p - (e+1)\,r_p]^{1/2}} =
\sqrt{G\,M}\,\,(t-\tau).$](img680.png) |
(4.54) |
Consider an elliptical orbit characterized by  . Let us write
. Let us write
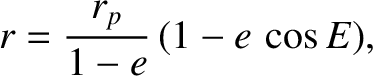 |
(4.55) |
where  is termed the eccentric anomaly. In fact,
is termed the eccentric anomaly. In fact,  is an angle that
varies between
is an angle that
varies between 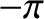 and
and 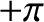 . Moreover, the perihelion point corresponds to
. Moreover, the perihelion point corresponds to
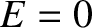 , and the aphelion point to
, and the aphelion point to 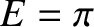 . Now,
. Now,
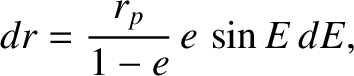 |
(4.56) |
whereas
 |
(4.57) |
Thus, Equation (4.54) reduces to
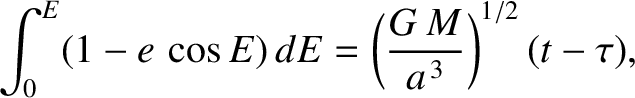 |
(4.58) |
where
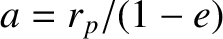 . This equation can immediately be integrated to give
. This equation can immediately be integrated to give
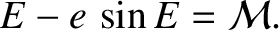 |
(4.59) |
Here,
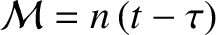 |
(4.60) |
is termed the mean anomaly,
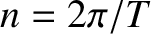 is the mean orbital angular velocity, and
is the mean orbital angular velocity, and
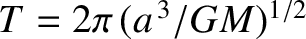 the orbital period. The mean anomaly is an angle that increases
uniformly in time at the rate of
the orbital period. The mean anomaly is an angle that increases
uniformly in time at the rate of 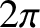 radians every orbital period.
Moreover, the perihelion point corresponds to
radians every orbital period.
Moreover, the perihelion point corresponds to
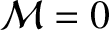 , and the aphelion point to
, and the aphelion point to
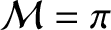 . Incidentally, the angle
. Incidentally, the angle
 , which determines the true angular location of the planet relative to its perihelion point, is called the
true anomaly.
Equation (4.59),
which is known as Kepler's equation, is a transcendental equation
that does not possess a convenient analytic solution. Fortunately, it is fairly straightforward to
solve numerically. For instance, when we use an iterative approach,
if
, which determines the true angular location of the planet relative to its perihelion point, is called the
true anomaly.
Equation (4.59),
which is known as Kepler's equation, is a transcendental equation
that does not possess a convenient analytic solution. Fortunately, it is fairly straightforward to
solve numerically. For instance, when we use an iterative approach,
if 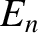 is the
is the  th guess then
th guess then
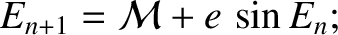 |
(4.61) |
this iteration scheme converges very rapidly when
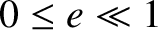 (as is the case for planetary orbits).
(as is the case for planetary orbits).
Figure 4.5:
Eccentric anomaly.
|
|
Equations (4.51) and (4.55) can be combined to give
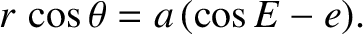 |
(4.62) |
This expression allows us to give a simple geometric interpretation of the eccentric anomaly,  .
Consider Figure 4.5. Let
.
Consider Figure 4.5. Let 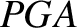 represent the elliptical orbit of a planet,
represent the elliptical orbit of a planet, 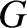 , about the Sun,
, about the Sun, 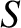 .
Let
.
Let 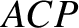 be the major axis of the orbit, where
be the major axis of the orbit, where 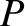 is the perihelion point,
is the perihelion point,  the aphelion point, and
the aphelion point, and
 the geometric center. It follows that
the geometric center. It follows that  and
and 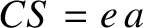 (see Section A.9), where
(see Section A.9), where  is the orbital major radius and
is the orbital major radius and  the
eccentricity. Moreover, the distance
the
eccentricity. Moreover, the distance 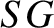 and the angle
and the angle 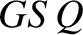 correspond to the radial distance,
correspond to the radial distance,  , and the
true anomaly,
, and the
true anomaly,  , respectively. Let
, respectively. Let 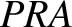 be a circle of radius
be a circle of radius  centered on
centered on  . It follows that
. It follows that  is
a diameter of this circle. Let
is
a diameter of this circle. Let 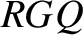 be a line, perpendicular to
be a line, perpendicular to  , that passes through
, that passes through 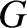 and joins the
circle to the diameter. It follows that
and joins the
circle to the diameter. It follows that 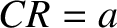 . Let us denote the angle
. Let us denote the angle  as
as  . Simple trigonometry
reveals that
. Simple trigonometry
reveals that
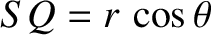 and
and
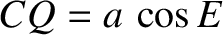 . But,
. But, 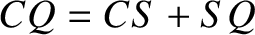 , or
, or
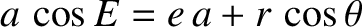 , which can be
rearranged to give
, which can be
rearranged to give
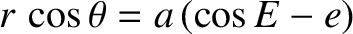 , which is identical to Equation (4.62). We, thus, conclude that the
eccentric anomaly,
, which is identical to Equation (4.62). We, thus, conclude that the
eccentric anomaly,  , can be identified with the angle
, can be identified with the angle  in Figure 4.5.
in Figure 4.5.
Equations (4.51) and (4.55) can be combined
to give
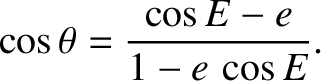 |
(4.63) |
Thus,
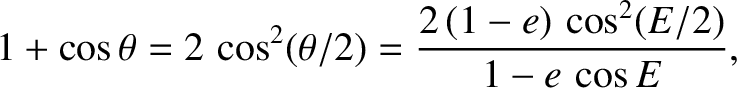 |
(4.64) |
and
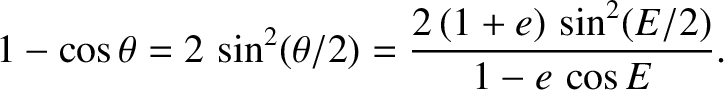 |
(4.65) |
The previous two equations imply that
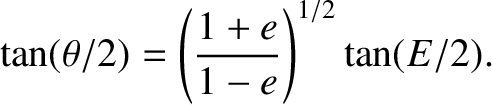 |
(4.66) |
The eccentric anomaly,  , and the true anomaly,
, and the true anomaly,  , always lie in the same quadrant (i.e., if
, always lie in the same quadrant (i.e., if
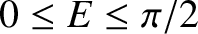 then
then
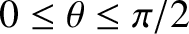 , etc.)
We conclude that, in the case of a planet in an elliptical orbit around the Sun, the radial distance,
, etc.)
We conclude that, in the case of a planet in an elliptical orbit around the Sun, the radial distance,  , and the
true anomaly,
, and the
true anomaly,  , are specified as functions of time via the solution of the following set of equations:
Here,
, are specified as functions of time via the solution of the following set of equations:
Here, 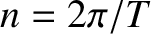 ,
,
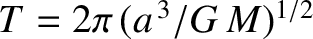 , and
, and
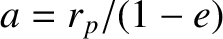 . Incidentally, it is clear that if
. Incidentally, it is clear that if
 then
then
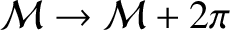 ,
,
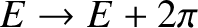 , and
, and
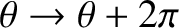 . In other words, the motion is periodic with period
. In other words, the motion is periodic with period
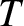 .
.
 and
and  , respectively, of
a planet in an elliptical orbit about the Sun as a function of time.
Suppose that the planet
passes through its perihelion point,
, respectively, of
a planet in an elliptical orbit about the Sun as a function of time.
Suppose that the planet
passes through its perihelion point, 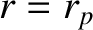 and
and 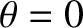 , at
, at 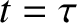 .
The constant
.
The constant 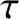 is termed the time of perihelion passage. It
follows from the previous analysis that
and
is termed the time of perihelion passage. It
follows from the previous analysis that
and
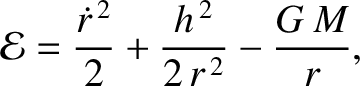
 ,
,
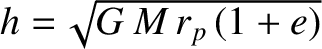 , and
, and
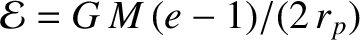 are the orbital eccentricity, angular momentum per unit mass, and
energy per unit mass, respectively. The preceding equation can be rearranged to
give
are the orbital eccentricity, angular momentum per unit mass, and
energy per unit mass, respectively. The preceding equation can be rearranged to
give
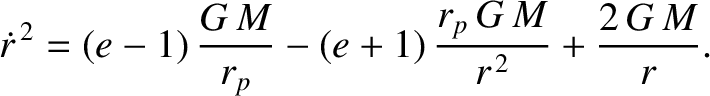
 . Let us write
. Let us write
 is termed the eccentric anomaly. In fact,
is termed the eccentric anomaly. In fact,  is an angle that
varies between
is an angle that
varies between 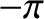 and
and 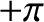 . Moreover, the perihelion point corresponds to
. Moreover, the perihelion point corresponds to
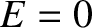 , and the aphelion point to
, and the aphelion point to 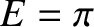 . Now,
. Now,
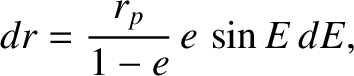

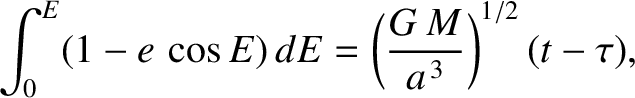
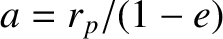 . This equation can immediately be integrated to give
Here,
is termed the mean anomaly,
. This equation can immediately be integrated to give
Here,
is termed the mean anomaly,
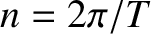 is the mean orbital angular velocity, and
is the mean orbital angular velocity, and
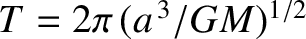 the orbital period. The mean anomaly is an angle that increases
uniformly in time at the rate of
the orbital period. The mean anomaly is an angle that increases
uniformly in time at the rate of 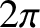 radians every orbital period.
Moreover, the perihelion point corresponds to
radians every orbital period.
Moreover, the perihelion point corresponds to
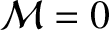 , and the aphelion point to
, and the aphelion point to
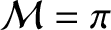 . Incidentally, the angle
. Incidentally, the angle
 , which determines the true angular location of the planet relative to its perihelion point, is called the
true anomaly.
Equation (4.59),
which is known as Kepler's equation, is a transcendental equation
that does not possess a convenient analytic solution. Fortunately, it is fairly straightforward to
solve numerically. For instance, when we use an iterative approach,
if
, which determines the true angular location of the planet relative to its perihelion point, is called the
true anomaly.
Equation (4.59),
which is known as Kepler's equation, is a transcendental equation
that does not possess a convenient analytic solution. Fortunately, it is fairly straightforward to
solve numerically. For instance, when we use an iterative approach,
if 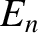 is the
is the  th guess then
th guess then
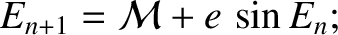
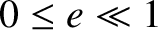 (as is the case for planetary orbits).
(as is the case for planetary orbits).
 .
Consider Figure 4.5. Let
.
Consider Figure 4.5. Let 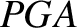 represent the elliptical orbit of a planet,
represent the elliptical orbit of a planet, 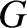 , about the Sun,
, about the Sun, 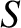 .
Let
.
Let 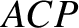 be the major axis of the orbit, where
be the major axis of the orbit, where 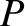 is the perihelion point,
is the perihelion point,  the aphelion point, and
the aphelion point, and
 the geometric center. It follows that
the geometric center. It follows that  and
and 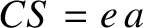 (see Section A.9), where
(see Section A.9), where  is the orbital major radius and
is the orbital major radius and  the
eccentricity. Moreover, the distance
the
eccentricity. Moreover, the distance 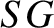 and the angle
and the angle 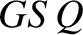 correspond to the radial distance,
correspond to the radial distance,  , and the
true anomaly,
, and the
true anomaly,  , respectively. Let
, respectively. Let 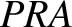 be a circle of radius
be a circle of radius  centered on
centered on  . It follows that
. It follows that  is
a diameter of this circle. Let
is
a diameter of this circle. Let 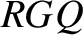 be a line, perpendicular to
be a line, perpendicular to  , that passes through
, that passes through 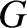 and joins the
circle to the diameter. It follows that
and joins the
circle to the diameter. It follows that 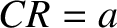 . Let us denote the angle
. Let us denote the angle  as
as  . Simple trigonometry
reveals that
. Simple trigonometry
reveals that
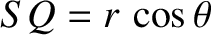 and
and
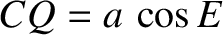 . But,
. But, 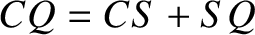 , or
, or
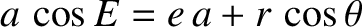 , which can be
rearranged to give
, which can be
rearranged to give
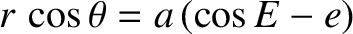 , which is identical to Equation (4.62). We, thus, conclude that the
eccentric anomaly,
, which is identical to Equation (4.62). We, thus, conclude that the
eccentric anomaly,  , can be identified with the angle
, can be identified with the angle  in Figure 4.5.
in Figure 4.5.
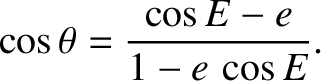
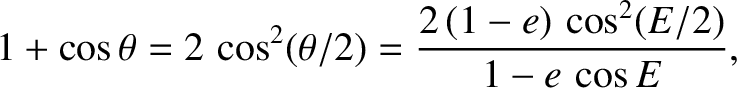
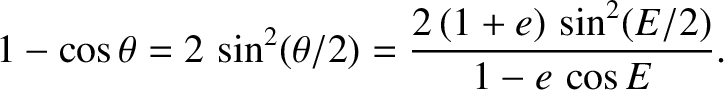
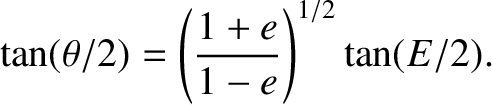
 , and the true anomaly,
, and the true anomaly,  , always lie in the same quadrant (i.e., if
, always lie in the same quadrant (i.e., if
 then
then
 , etc.)
We conclude that, in the case of a planet in an elliptical orbit around the Sun, the radial distance,
, etc.)
We conclude that, in the case of a planet in an elliptical orbit around the Sun, the radial distance,  , and the
true anomaly,
, and the
true anomaly,  , are specified as functions of time via the solution of the following set of equations:
Here,
, are specified as functions of time via the solution of the following set of equations:
Here, 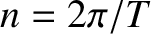 ,
,
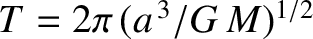 , and
, and
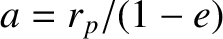 . Incidentally, it is clear that if
. Incidentally, it is clear that if
 then
then
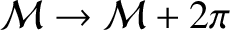 ,
,
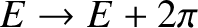 , and
, and
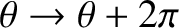 . In other words, the motion is periodic with period
. In other words, the motion is periodic with period
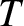 .
.