Next: Time evolution of eccentricity Up: Perihelion precession of Mercury Previous: Perihelion precession of Mercury
Let  and
and 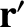 be the position vectors of Mercury and some other planet in the solar system, respectively, relative to the Sun.
Furthermore, let
be the position vectors of Mercury and some other planet in the solar system, respectively, relative to the Sun.
Furthermore, let  ,
, 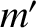 , and
, and  be the masses of Mercury, the other planet, and the Sun, respectively.
According to the analysis of Section 10.2, the vector
be the masses of Mercury, the other planet, and the Sun, respectively.
According to the analysis of Section 10.2, the vector  evolves in time according to
evolves in time according to
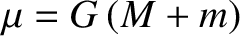 . Here, the disturbing function due to the
other planet takes the form
. Here, the disturbing function due to the
other planet takes the form
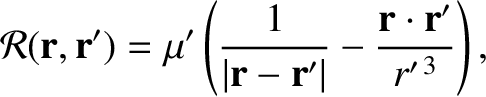 |
(B.2) |
 .
.