Perihelion precession of Mercury
As described in Appendix B, if the calculation described in the previous section is carried out more accurately, taking into account the slight
eccentricities of the planetary orbits, as well as their small mutual inclinations, then the perihelion
precession rate of the planet Mercury is found to be 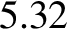 arc seconds per year. However, the
observed precession rate is
arc seconds per year. However, the
observed precession rate is 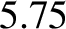 arc seconds per year. It turns out that the
cause of this discrepancy is a general relativistic correction to Newtonian gravity.
arc seconds per year. It turns out that the
cause of this discrepancy is a general relativistic correction to Newtonian gravity.
General relativity gives rise to a small correction to the force per unit mass
exerted by the Sun (mass  ) on a planet in a circular orbit of radius
) on a planet in a circular orbit of radius  , and angular momentum
per unit mass
, and angular momentum
per unit mass  . This correction is due to the curvature of space in the immediate vicinity of the Sun.
In fact, the modified formula for
. This correction is due to the curvature of space in the immediate vicinity of the Sun.
In fact, the modified formula for  is (Rindler 1977)
is (Rindler 1977)
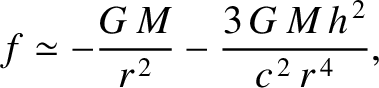 |
(5.26) |
where 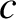 is the velocity of light in vacuum. It follows that
is the velocity of light in vacuum. It follows that
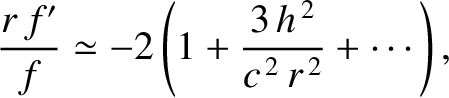 |
(5.27) |
to first order in
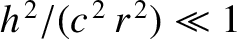 .
Hence, from Equation (5.19), the apsidal angle is
.
Hence, from Equation (5.19), the apsidal angle is
 |
(5.28) |
Thus, the perihelion advances by
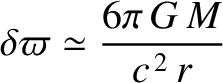 |
(5.29) |
radians per revolution due to the general relativistic correction to Newtonian gravity. Here,
use has been made of
 . It follows that the
rate of perihelion precession due to the general relativistic correction is
. It follows that the
rate of perihelion precession due to the general relativistic correction is
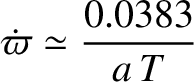 |
(5.30) |
arc seconds per year, where  is the mean orbital radius in astronomical units,
and
is the mean orbital radius in astronomical units,
and 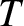 the orbital period in years. Hence, from Table 4.1, the general relativistic contribution to
the orbital period in years. Hence, from Table 4.1, the general relativistic contribution to
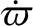 for Mercury is
for Mercury is
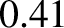 arc seconds per year. It is easily demonstrated that the corresponding contributions are fairly negligible for
the other planets in the solar system. If the preceding calculation is carried out sightly more accurately,
taking the eccentricity of Mercury's orbit into account, then the general relativistic contribution
to
arc seconds per year. It is easily demonstrated that the corresponding contributions are fairly negligible for
the other planets in the solar system. If the preceding calculation is carried out sightly more accurately,
taking the eccentricity of Mercury's orbit into account, then the general relativistic contribution
to
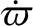 becomes
becomes
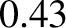 arc seconds per year. (See Exercise 2.) It follows that the total perihelion precession rate for Mercury
is
arc seconds per year. (See Exercise 2.) It follows that the total perihelion precession rate for Mercury
is
 arc seconds per year. This is in exact agreement with the observed precession
rate. Indeed, the ability of general relativity to explain the discrepancy between the observed perihelion precession
rate of Mercury, and that calculated from Newtonian mechanics, was one of the first major successful tests of
this theory.
arc seconds per year. This is in exact agreement with the observed precession
rate. Indeed, the ability of general relativity to explain the discrepancy between the observed perihelion precession
rate of Mercury, and that calculated from Newtonian mechanics, was one of the first major successful tests of
this theory.
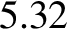 arc seconds per year. However, the
observed precession rate is
arc seconds per year. However, the
observed precession rate is 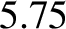 arc seconds per year. It turns out that the
cause of this discrepancy is a general relativistic correction to Newtonian gravity.
arc seconds per year. It turns out that the
cause of this discrepancy is a general relativistic correction to Newtonian gravity.
 ) on a planet in a circular orbit of radius
) on a planet in a circular orbit of radius  , and angular momentum
per unit mass
, and angular momentum
per unit mass 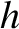 . This correction is due to the curvature of space in the immediate vicinity of the Sun.
In fact, the modified formula for
. This correction is due to the curvature of space in the immediate vicinity of the Sun.
In fact, the modified formula for 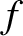 is (Rindler 1977)
is (Rindler 1977)
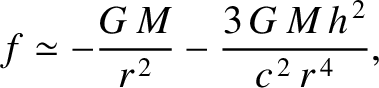
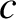 is the velocity of light in vacuum. It follows that
is the velocity of light in vacuum. It follows that
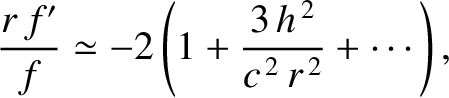
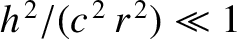 .
Hence, from Equation (5.19), the apsidal angle is
.
Hence, from Equation (5.19), the apsidal angle is

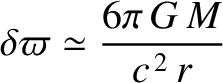
 . It follows that the
rate of perihelion precession due to the general relativistic correction is
. It follows that the
rate of perihelion precession due to the general relativistic correction is
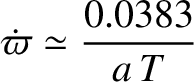
 is the mean orbital radius in astronomical units,
and
is the mean orbital radius in astronomical units,
and 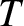 the orbital period in years. Hence, from Table 4.1, the general relativistic contribution to
the orbital period in years. Hence, from Table 4.1, the general relativistic contribution to
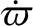 for Mercury is
for Mercury is
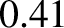 arc seconds per year. It is easily demonstrated that the corresponding contributions are fairly negligible for
the other planets in the solar system. If the preceding calculation is carried out sightly more accurately,
taking the eccentricity of Mercury's orbit into account, then the general relativistic contribution
to
arc seconds per year. It is easily demonstrated that the corresponding contributions are fairly negligible for
the other planets in the solar system. If the preceding calculation is carried out sightly more accurately,
taking the eccentricity of Mercury's orbit into account, then the general relativistic contribution
to
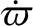 becomes
becomes
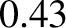 arc seconds per year. (See Exercise 2.) It follows that the total perihelion precession rate for Mercury
is
arc seconds per year. (See Exercise 2.) It follows that the total perihelion precession rate for Mercury
is
 arc seconds per year. This is in exact agreement with the observed precession
rate. Indeed, the ability of general relativity to explain the discrepancy between the observed perihelion precession
rate of Mercury, and that calculated from Newtonian mechanics, was one of the first major successful tests of
this theory.
arc seconds per year. This is in exact agreement with the observed precession
rate. Indeed, the ability of general relativity to explain the discrepancy between the observed perihelion precession
rate of Mercury, and that calculated from Newtonian mechanics, was one of the first major successful tests of
this theory.