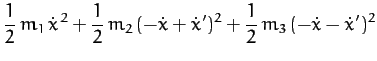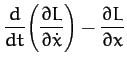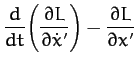

Next: Sliding down a Sliding
Up: Lagrangian Dynamics
Previous: Motion in a Central
An Atwood machine consists of two weights, of mass 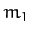 and
and 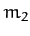 ,
connected by a light inextensible cord of length
,
connected by a light inextensible cord of length 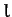 , which passes over
a pulley of radius
, which passes over
a pulley of radius 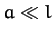 , and moment of inertia
, and moment of inertia 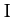 . See Figure 32.
. See Figure 32.
Figure 32:
An Atwood machine.
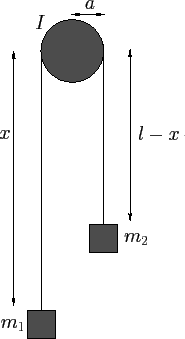 |
Referring to the diagram, we can see that this is a one degree of freedom
system whose instantaneous configuration is specified by the coordinate 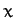 .
Assuming that the cord does not slip with respect to the pulley, the
angular velocity of pulley is
.
Assuming that the cord does not slip with respect to the pulley, the
angular velocity of pulley is 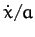 . Hence, the kinetic
energy of the system is given by
. Hence, the kinetic
energy of the system is given by
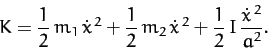 |
(624) |
The potential energy of the system takes the form
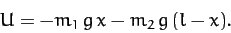 |
(625) |
It follows that the Lagrangian is written
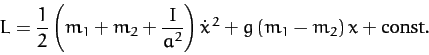 |
(626) |
The equation of motion,
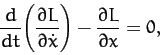 |
(627) |
thus yields
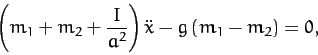 |
(628) |
or
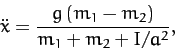 |
(629) |
which is the correct answer.
Figure 33:
A double Atwood machine.
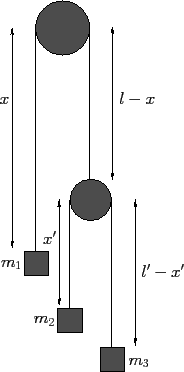 |
Consider the dynamical system drawn in Figure 33. This is an Atwood
machine in which one of the weights has been replaced by a second
Atwood machine with a cord of length 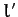 . The system now has two degrees of freedom, and
its instantaneous position is specified by the two coordinates
. The system now has two degrees of freedom, and
its instantaneous position is specified by the two coordinates 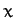 and
and 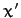 ,
as shown.
,
as shown.
For the sake of simplicity, let us neglect the masses of the two pulleys.
Thus, the kinetic energy of the system is written
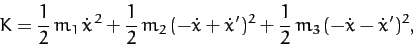 |
(630) |
whereas the potential energy takes the form
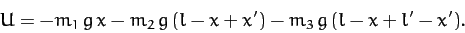 |
(631) |
It follows that the Lagrangian of the system is
Hence, the equations of motion,
yield
The accelerations 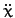 and
and 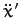 can be obtained from
the above two equations via simple algebra.
can be obtained from
the above two equations via simple algebra.


Next: Sliding down a Sliding
Up: Lagrangian Dynamics
Previous: Motion in a Central
Richard Fitzpatrick
2011-03-31

![]() .
Assuming that the cord does not slip with respect to the pulley, the
angular velocity of pulley is
.
Assuming that the cord does not slip with respect to the pulley, the
angular velocity of pulley is ![]() . Hence, the kinetic
energy of the system is given by
. Hence, the kinetic
energy of the system is given by
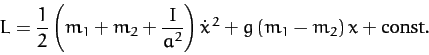
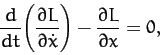
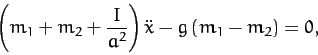
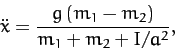
![]() . The system now has two degrees of freedom, and
its instantaneous position is specified by the two coordinates
. The system now has two degrees of freedom, and
its instantaneous position is specified by the two coordinates ![]() and
and ![]() ,
as shown.
,
as shown.