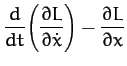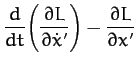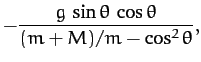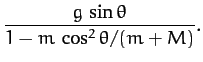Next: Generalized Momenta
Up: Lagrangian Dynamics
Previous: Atwood Machines
Sliding down a Sliding Plane
Consider the case of a particle of mass 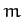 sliding down a smooth
inclined plane of mass
sliding down a smooth
inclined plane of mass 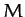 which is, itself, free to slide on
a smooth horizontal surface, as shown in Figure 34.
This is a two degree of freedom system, so we need two
coordinates to specify the configuration. Let us choose
which is, itself, free to slide on
a smooth horizontal surface, as shown in Figure 34.
This is a two degree of freedom system, so we need two
coordinates to specify the configuration. Let us choose  ,
the horizontal distance of the plane from some reference point, and
,
the horizontal distance of the plane from some reference point, and
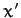 , the parallel displacement of the particle from some reference point
on the plane.
, the parallel displacement of the particle from some reference point
on the plane.
Figure 34:
A sliding plane.
 |
Defining  - and
- and  -axes, as shown in the diagram, the
-axes, as shown in the diagram, the  - and
- and
 -components of the particle's velocity are clearly given by
-components of the particle's velocity are clearly given by
respectively, where  is the angle of inclination of the plane with
respect to the horizontal.
Thus,
is the angle of inclination of the plane with
respect to the horizontal.
Thus,
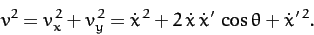 |
(639) |
Hence, the kinetic energy of the system takes the form
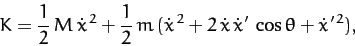 |
(640) |
whereas the potential energy is given by
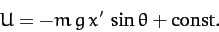 |
(641) |
It follows that the Lagrangian is written
 |
(642) |
The equations of motion,
thus yield
Finally, solving for 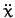 and
and 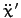 , we obtain
, we obtain



Next: Generalized Momenta
Up: Lagrangian Dynamics
Previous: Atwood Machines
Richard Fitzpatrick
2011-03-31

![]() - and
- and ![]() -axes, as shown in the diagram, the
-axes, as shown in the diagram, the ![]() - and
- and
![]() -components of the particle's velocity are clearly given by
-components of the particle's velocity are clearly given by