


Next: Scattering in the Laboratory
Up: Two-Body Dynamics
Previous: Binary Star Systems
Scattering in the Center of Mass Frame
Let us now consider scattering due to the collision of two particles. We shall
restrict our discussion to particles which interact via conservative central
forces. It turns out that scattering looks particularly simple when
viewed in the center of mass frame. Let us, therefore, start our investigation
by considering two-particle scattering in the center of mass frame.
As before, the first particle is of mass 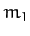 , and is located at position
vector
, and is located at position
vector 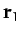 , whereas the second particle is of mass
, whereas the second particle is of mass 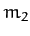 ,
and is located at
,
and is located at 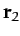 .
By definition, there is zero net linear momentum in the center of mass
frame at all times. Hence, if the first particle approaches the collision
point with momentum
.
By definition, there is zero net linear momentum in the center of mass
frame at all times. Hence, if the first particle approaches the collision
point with momentum 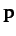 then the second must approach
with momentum
then the second must approach
with momentum 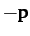 . Likewise, after the collision, if the
first particle recedes from the collision point with momentum
. Likewise, after the collision, if the
first particle recedes from the collision point with momentum 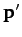 then the second must recede with momentum
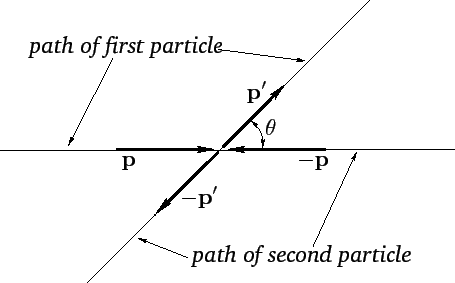
then the second must recede with momentum 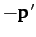 --see Figure 21. Furthermore, since the interaction force is
conservative, the total kinetic energy before and after the collision must
be the same. It follows that the magnitude of the final momentum
vector,
--see Figure 21. Furthermore, since the interaction force is
conservative, the total kinetic energy before and after the collision must
be the same. It follows that the magnitude of the final momentum
vector, 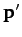 , is equal to the magnitude of the initial momentum vector,
, is equal to the magnitude of the initial momentum vector, 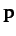 . Because of this, the collision event is completely specified
once the angle
. Because of this, the collision event is completely specified
once the angle  through which the
first particle is scattered is given. Of course, in the center of mass frame, the second particle
is scattered through the same angle--see Figure 21.
through which the
first particle is scattered is given. Of course, in the center of mass frame, the second particle
is scattered through the same angle--see Figure 21.
Figure 21:
A collision viewed in the center of mass frame.
 |
Suppose that the two particles interact via the potential 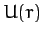 , where
, where 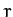 is the distance separating the particles. As we have seen, the two-body
problem sketched in Figure 21 can be converted into the
equivalent one-body problem sketched in Figure 22. In this
equivalent problem, a particle of mass
is the distance separating the particles. As we have seen, the two-body
problem sketched in Figure 21 can be converted into the
equivalent one-body problem sketched in Figure 22. In this
equivalent problem, a particle of mass
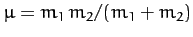 is scattered
in the fixed potential
is scattered
in the fixed potential 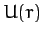 , where
, where 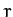 is now the distance from the origin.
The vector position
is now the distance from the origin.
The vector position 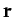 of the particle in the equivalent problem corresponds to the relative position vector
of the particle in the equivalent problem corresponds to the relative position vector
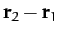 in the original problem.
It follows that the angle
in the original problem.
It follows that the angle  through which the particle is scattered in the equivalent
problem is the same as the scattering angle
through which the particle is scattered in the equivalent
problem is the same as the scattering angle  in the original problem.
in the original problem.
Figure 22:
The one-body equivalent to the previous figure.
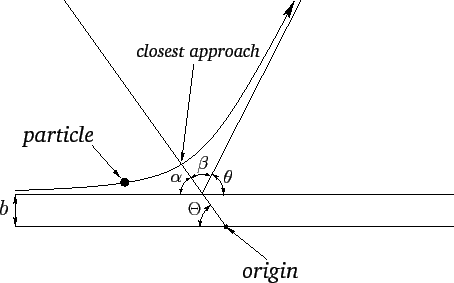 |
The scattering angle,  , is largely
determined by the so-called impact parameter,
, is largely
determined by the so-called impact parameter, 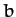 , which is the
distance of closest approach of the two particles in the absence of an
interaction potential. In the equivalent problem,
, which is the
distance of closest approach of the two particles in the absence of an
interaction potential. In the equivalent problem, 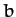 is the distance of
closest approach to the origin in the absence of an interaction
potential--see Figure 22. If
is the distance of
closest approach to the origin in the absence of an interaction
potential--see Figure 22. If 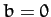 then we have a head-on collision. In this case, we expect
the two particles to reverse direction after colliding: i.e., we expect
then we have a head-on collision. In this case, we expect
the two particles to reverse direction after colliding: i.e., we expect
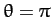 . Likewise, if
. Likewise, if 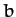 is large then we expect the two particles
to miss one another entirely, in which case
is large then we expect the two particles
to miss one another entirely, in which case 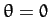 . It follows that the
scattering angle,
. It follows that the
scattering angle,  , is a decreasing function of the impact parameter,
, is a decreasing function of the impact parameter,
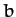 .
.
Suppose that the polar coordinates of the particle in the equivalent problem
are
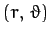 . Let the particle approach the origin from the direction
. Let the particle approach the origin from the direction
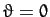 , and attain its closest distance to the origin when
, and attain its closest distance to the origin when
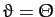 . From symmetry, the angle
. From symmetry, the angle 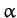 in Figure 22 is equal to the angle
in Figure 22 is equal to the angle 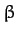 . However, from simple geometry,
. However, from simple geometry,
 . Hence,
. Hence,
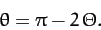 |
(340) |
Now, by analogy with Equation (267), the conserved total energy 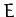 in the equivalent
problem, which can easily be shown to be the same as the total energy in
the original problem, is given by
in the equivalent
problem, which can easily be shown to be the same as the total energy in
the original problem, is given by
![\begin{displaymath}
E = \frac{\mu\,h^2}{2}\left[\left(\frac{du}{d\vartheta}\right)^2 + u^2\right] + U(u),
\end{displaymath}](img961.png) |
(341) |
where 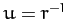 , and
, and 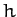 is the angular momentum per unit mass in the
equivalent problem. It is easily seen that
is the angular momentum per unit mass in the
equivalent problem. It is easily seen that
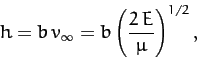 |
(342) |
where 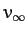 is the approach velocity in the equivalent problem
at large
is the approach velocity in the equivalent problem
at large 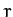 .
It follows that
.
It follows that
![\begin{displaymath}
E = E\,b^2\left[\left(\frac{du}{d\vartheta}\right)^2 + u^2\right] + U(u).
\end{displaymath}](img964.png) |
(343) |
The above equation can be rearranged to
give
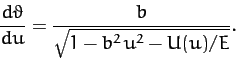 |
(344) |
Integration yields
 |
(345) |
Here,
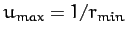 , where
, where 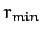 is the distance of closest approach. Since, by symmetry,
is the distance of closest approach. Since, by symmetry,
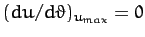 , it follows from Equation (344) that
, it follows from Equation (344) that
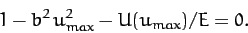 |
(346) |
Equations (340) and (345) enable us to calculate the
function 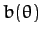 for a given interaction potential,
for a given interaction potential, 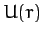 , and a
given total energy,
, and a
given total energy, 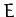 , of the two particles in the center of mass frame. The function
, of the two particles in the center of mass frame. The function 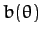 tells us which impact parameter corresponds to which scattering angle,
and vice versa.
tells us which impact parameter corresponds to which scattering angle,
and vice versa.
Instead of two particles, suppose that we now have two counter-propagating beams of identical particles (with the same properties as the
two particles described above) which scatter one another via binary collisions. What
is the angular distribution of the scattered particles?
Consider pairs of particles whose impact parameters lie in the range 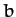 to
to 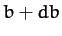 . These particles are scattered in such a manner that their scattering
angles lie in the range
. These particles are scattered in such a manner that their scattering
angles lie in the range  to
to
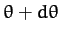 , where
, where  is determined from inverting the function
is determined from inverting the function 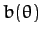 , and
, and
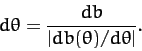 |
(347) |
Incidentally, we must take the modulus of
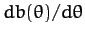 because
because 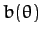 is
a decreasing function of
is
a decreasing function of  . Assuming, as seems reasonable, that the scattering
is azimuthally symmetric, the range of solid angle into which
the particles are scattered is
. Assuming, as seems reasonable, that the scattering
is azimuthally symmetric, the range of solid angle into which
the particles are scattered is
 |
(348) |
Finally, the cross-sectional area of the annulus through which incoming
particles must pass if they are to have impact parameters in the
range 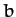 to
to 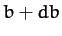 is
is
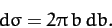 |
(349) |
The previous two equations allow us to define the differential scattering
cross-section:
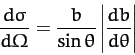 |
(350) |
The differential scattering cross-section has units of area per steradian,
and specifies the effective target area for scattering into a given
range of solid angle. For two uniform beams scattering
off one another, the differential scattering cross-section thus
effectively specifies the probability of scattering into a given range of
solid angle. The total scattering cross-section is the integral
of the differential cross-section over all solid angles,
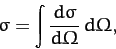 |
(351) |
and measures the effective target area for scattering in any direction.
Thus, if the flux of particles per unit area per unit time, otherwise known as the intensity, of the two beams is 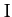 , then the number of particles of a given type scattered
per unit time is simply
, then the number of particles of a given type scattered
per unit time is simply 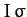 .
.
Let us now calculate the scattering cross-section for the following
very simple interaction potential:
![\begin{displaymath}
U(r) =
\left\{\begin{array}{lll}
0&\mbox{\hspace{1cm}} & r>a\\ [0.5ex]
\infty && r\leq a
\end{array}\right..
\end{displaymath}](img981.png) |
(352) |
This is the interaction potential of impenetrable spheres which only
exert a force on one another when they are in physical contact
(e.g., billiard balls). If the particles in the first beam have
radius  , and the particles in the second beam have radius
, and the particles in the second beam have radius 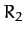 ,
then
,
then 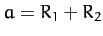 . In other words, the centers of two particles, one from either
beam, can never be less than a distance
. In other words, the centers of two particles, one from either
beam, can never be less than a distance 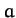 apart, where
apart, where
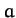 is the sum of their radii (since the particles
are impenetrable spheres).
is the sum of their radii (since the particles
are impenetrable spheres).
Equations (340), (345), and (352)
yield
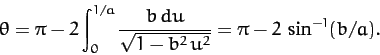 |
(353) |
The above formula can be rearranged to give
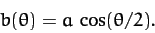 |
(354) |
Note that
 |
(355) |
Hence, Equations (350) and (355) yield
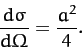 |
(356) |
We thus conclude that when two beams of impenetrable spheres
collide, in the center of mass frame, the particles in the two beams have
an equal probability of being scattered in any direction. The total scattering
cross-section is
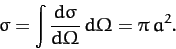 |
(357) |
Obviously, this result makes a lot of sense--the total scattering cross-section
for two impenetrable spheres is simply the area of a circle
whose radius is the sum of the radii of the two spheres.
Let us now consider scattering by an inverse-square interaction force
whose potential takes the form
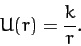 |
(358) |
It follows from Equations (345) and (346) that
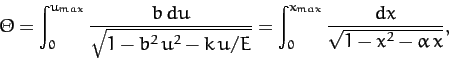 |
(359) |
where
 , and
, and
 |
(360) |
Integration yields
 |
(361) |
Hence, from Equation (340), we obtain
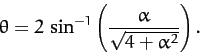 |
(362) |
The above equation can be rearranged to give
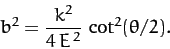 |
(363) |
Thus,
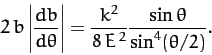 |
(364) |
Finally, using Equation (350), we get
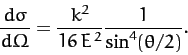 |
(365) |
There are a number of things to note about the above formula. First, the
scattering cross-section is proportional to 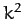 . This means that
repulsive (
. This means that
repulsive (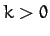 ) and attractive (
) and attractive (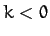 ) inverse-square interaction forces
of the same strength give rise to identical angular distributions of scattered
particles. Second, the scattering cross-section is proportional to
) inverse-square interaction forces
of the same strength give rise to identical angular distributions of scattered
particles. Second, the scattering cross-section is proportional to 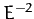 .
This means that inverse-square interaction forces are much
more effective at scattering low energy, rather than high energy, particles.
Finally, the differential scattering cross-section is proportional to
.
This means that inverse-square interaction forces are much
more effective at scattering low energy, rather than high energy, particles.
Finally, the differential scattering cross-section is proportional to
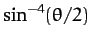 . This means that, with an inverse-square
interaction force, the overwhelming majority of
``collisions'' consist of small angle scattering events (i.e.,
. This means that, with an inverse-square
interaction force, the overwhelming majority of
``collisions'' consist of small angle scattering events (i.e., 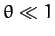 ).
).
Let us now consider a specific case. Suppose that we have particles
of electric charge 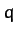 scattering off particles of the same charge. The
interaction potential due to the Coulomb force between the particles
is simply
scattering off particles of the same charge. The
interaction potential due to the Coulomb force between the particles
is simply
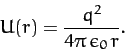 |
(366) |
Thus, it follows from Equation (365) [with
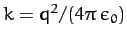 ]
that the differential scattering cross-section takes the form
]
that the differential scattering cross-section takes the form
 |
(367) |
This very famous formula is known as the Rutherford scattering cross-section, since it was first derived by Earnst Rutherford for use in his
celebrated 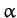 -particle scattering experiment.
-particle scattering experiment.
Note, finally, that if we try to integrate the Rutherford formula to obtain
the total scattering cross-section then we find that the integral is divergent,
due to the very strong increase in
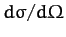 as
as
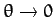 . This implies that the Coulomb potential (or any
other inverse-square-law potential)
has an effectively infinite range. In practice, however, an electric
charge is generally surrounded by charges of the opposite sign which
shield the Coulomb potential of the charge beyond a certain distance.
This shielding effect allows the charge to have a finite total
scattering cross-section (for the scattering of other electric charges). However, the total scattering cross-section of the charge
depends (albeit, logarithmically) on the shielding distance, and, hence, on the
nature and distribution of the charges surrounding it.
. This implies that the Coulomb potential (or any
other inverse-square-law potential)
has an effectively infinite range. In practice, however, an electric
charge is generally surrounded by charges of the opposite sign which
shield the Coulomb potential of the charge beyond a certain distance.
This shielding effect allows the charge to have a finite total
scattering cross-section (for the scattering of other electric charges). However, the total scattering cross-section of the charge
depends (albeit, logarithmically) on the shielding distance, and, hence, on the
nature and distribution of the charges surrounding it.



Next: Scattering in the Laboratory
Up: Two-Body Dynamics
Previous: Binary Star Systems
Richard Fitzpatrick
2011-03-31
![]() , and is located at position
vector
, and is located at position
vector ![]() , whereas the second particle is of mass
, whereas the second particle is of mass ![]() ,
and is located at
,
and is located at ![]() .
By definition, there is zero net linear momentum in the center of mass
frame at all times. Hence, if the first particle approaches the collision
point with momentum
.
By definition, there is zero net linear momentum in the center of mass
frame at all times. Hence, if the first particle approaches the collision
point with momentum ![]() then the second must approach
with momentum
then the second must approach
with momentum ![]() . Likewise, after the collision, if the
first particle recedes from the collision point with momentum
. Likewise, after the collision, if the
first particle recedes from the collision point with momentum ![]() then the second must recede with momentum
then the second must recede with momentum ![]() --see Figure 21. Furthermore, since the interaction force is
conservative, the total kinetic energy before and after the collision must
be the same. It follows that the magnitude of the final momentum
vector,
--see Figure 21. Furthermore, since the interaction force is
conservative, the total kinetic energy before and after the collision must
be the same. It follows that the magnitude of the final momentum
vector, ![]() , is equal to the magnitude of the initial momentum vector,
, is equal to the magnitude of the initial momentum vector, ![]() . Because of this, the collision event is completely specified
once the angle
. Because of this, the collision event is completely specified
once the angle ![]() through which the
first particle is scattered is given. Of course, in the center of mass frame, the second particle
is scattered through the same angle--see Figure 21.
through which the
first particle is scattered is given. Of course, in the center of mass frame, the second particle
is scattered through the same angle--see Figure 21.
![]() , where
, where ![]() is the distance separating the particles. As we have seen, the two-body
problem sketched in Figure 21 can be converted into the
equivalent one-body problem sketched in Figure 22. In this
equivalent problem, a particle of mass
is the distance separating the particles. As we have seen, the two-body
problem sketched in Figure 21 can be converted into the
equivalent one-body problem sketched in Figure 22. In this
equivalent problem, a particle of mass
![]() is scattered
in the fixed potential
is scattered
in the fixed potential ![]() , where
, where ![]() is now the distance from the origin.
The vector position
is now the distance from the origin.
The vector position ![]() of the particle in the equivalent problem corresponds to the relative position vector
of the particle in the equivalent problem corresponds to the relative position vector
![]() in the original problem.
It follows that the angle
in the original problem.
It follows that the angle ![]() through which the particle is scattered in the equivalent
problem is the same as the scattering angle
through which the particle is scattered in the equivalent
problem is the same as the scattering angle ![]() in the original problem.
in the original problem.
![]() , is largely
determined by the so-called impact parameter,
, is largely
determined by the so-called impact parameter, ![]() , which is the
distance of closest approach of the two particles in the absence of an
interaction potential. In the equivalent problem,
, which is the
distance of closest approach of the two particles in the absence of an
interaction potential. In the equivalent problem, ![]() is the distance of
closest approach to the origin in the absence of an interaction
potential--see Figure 22. If
is the distance of
closest approach to the origin in the absence of an interaction
potential--see Figure 22. If ![]() then we have a head-on collision. In this case, we expect
the two particles to reverse direction after colliding: i.e., we expect
then we have a head-on collision. In this case, we expect
the two particles to reverse direction after colliding: i.e., we expect
![]() . Likewise, if
. Likewise, if ![]() is large then we expect the two particles
to miss one another entirely, in which case
is large then we expect the two particles
to miss one another entirely, in which case ![]() . It follows that the
scattering angle,
. It follows that the
scattering angle, ![]() , is a decreasing function of the impact parameter,
, is a decreasing function of the impact parameter,
![]() .
.
![]() . Let the particle approach the origin from the direction
. Let the particle approach the origin from the direction
![]() , and attain its closest distance to the origin when
, and attain its closest distance to the origin when
![]() . From symmetry, the angle
. From symmetry, the angle ![]() in Figure 22 is equal to the angle
in Figure 22 is equal to the angle ![]() . However, from simple geometry,
. However, from simple geometry,
![]() . Hence,
. Hence,
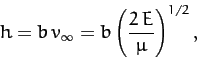
![]() to
to ![]() . These particles are scattered in such a manner that their scattering
angles lie in the range
. These particles are scattered in such a manner that their scattering
angles lie in the range ![]() to
to
![]() , where
, where ![]() is determined from inverting the function
is determined from inverting the function ![]() , and
, and
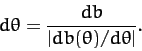

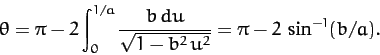
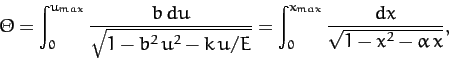

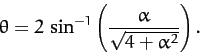
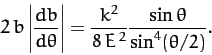
![]() scattering off particles of the same charge. The
interaction potential due to the Coulomb force between the particles
is simply
scattering off particles of the same charge. The
interaction potential due to the Coulomb force between the particles
is simply
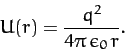
![]() as
as
![]() . This implies that the Coulomb potential (or any
other inverse-square-law potential)
has an effectively infinite range. In practice, however, an electric
charge is generally surrounded by charges of the opposite sign which
shield the Coulomb potential of the charge beyond a certain distance.
This shielding effect allows the charge to have a finite total
scattering cross-section (for the scattering of other electric charges). However, the total scattering cross-section of the charge
depends (albeit, logarithmically) on the shielding distance, and, hence, on the
nature and distribution of the charges surrounding it.
. This implies that the Coulomb potential (or any
other inverse-square-law potential)
has an effectively infinite range. In practice, however, an electric
charge is generally surrounded by charges of the opposite sign which
shield the Coulomb potential of the charge beyond a certain distance.
This shielding effect allows the charge to have a finite total
scattering cross-section (for the scattering of other electric charges). However, the total scattering cross-section of the charge
depends (albeit, logarithmically) on the shielding distance, and, hence, on the
nature and distribution of the charges surrounding it.