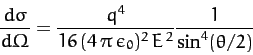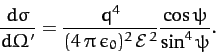Next: Exercises
Up: Two-Body Dynamics
Previous: Scattering in the Center
We have seen that two-particle scattering looks fairly simple when viewed in the
center of mass frame. Unfortunately, we are not usually in a position
to do this. In the laboratory, the most
common scattering scenario is one in which the second particle is
initially at rest. Let us now investigate this situation.
Suppose that, in the center of mass frame, the first particle has velocity
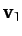 before the collision, and velocity
before the collision, and velocity 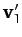 after the
collision. Likewise, the second particle has velocity
after the
collision. Likewise, the second particle has velocity  before the
collision, and
before the
collision, and 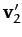 after the collision. We know that
after the collision. We know that
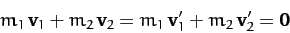 |
(368) |
in the center of mass frame. Moreover, since the collision is assumed to be elastic (i.e., energy conserving),
Let us transform
to a new inertial frame of reference--which we shall call the laboratory frame--which is moving with the uniform velocity 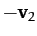 with respect to
the center of mass frame. In the new reference frame, the first
particle has initial velocity
with respect to
the center of mass frame. In the new reference frame, the first
particle has initial velocity
 , and
final velocity
, and
final velocity
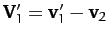 . Furthermore, the second particle
is initially at rest, and has the final velocity
. Furthermore, the second particle
is initially at rest, and has the final velocity
 . The relationship between scattering in the center of mass frame
and scattering in the laboratory frame is illustrated in Figure 23.
. The relationship between scattering in the center of mass frame
and scattering in the laboratory frame is illustrated in Figure 23.
Figure 23:
Scattering in the center of mass and laboratory frames.
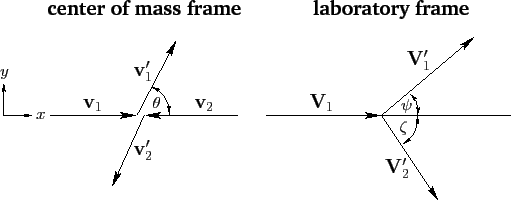 |
In the center of mass frame, both particles are scattered through the same angle  . However, in the laboratory frame, the first and second particles
are scattered by the (generally different) angles
. However, in the laboratory frame, the first and second particles
are scattered by the (generally different) angles 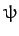 and
and 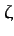 ,
respectively.
,
respectively.
Defining  - and
- and  -axes, as indicated in Figure 23, it is easily
seen that the Cartesian components of the various velocity vectors in the
two frames of reference are:
-axes, as indicated in Figure 23, it is easily
seen that the Cartesian components of the various velocity vectors in the
two frames of reference are:
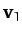 |
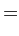 |
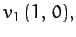 |
(371) |
 |
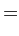 |
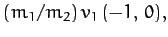 |
(372) |
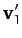 |
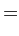 |
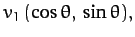 |
(373) |
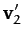 |
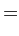 |
 |
(374) |
 |
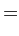 |
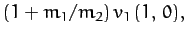 |
(375) |
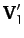 |
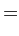 |
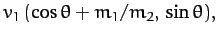 |
(376) |
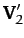 |
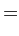 |
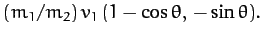 |
(377) |
In the center of mass frame, let 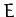 be the total energy, let
be the total energy, let
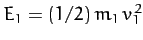 and
and
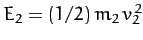 be the kinetic energies of the first and second particles, respectively, before the collision, and let
be the kinetic energies of the first and second particles, respectively, before the collision, and let
 and
and
 be the kinetic energies of the first and second particles, respectively, after the collision. Of course,
be the kinetic energies of the first and second particles, respectively, after the collision. Of course,
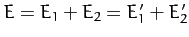 .
In the laboratory frame, let
.
In the laboratory frame, let  be the total energy. This is, of course,
equal to the kinetic energy of the first particle before the collision. Likewise,
let
be the total energy. This is, of course,
equal to the kinetic energy of the first particle before the collision. Likewise,
let
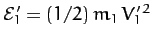 and
and
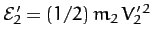 be the kinetic energies of the first and second particles, respectively, after the collision. Of course,
be the kinetic energies of the first and second particles, respectively, after the collision. Of course,
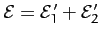 .
.
The following results can easily be obtained from the above definitions and
Equations (371)-(377). First,
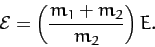 |
(378) |
Hence, the total energy in the laboratory frame is always greater than
that in the center of mass frame. In fact, it can be demonstrated that the
total energy in the center of mass frame is less than the total energy in any
other inertial frame. Second,
These equations specify how the total energy in the center of mass
frame is distributed
between the two particles. Note that this distribution is unchanged by the
collision.
Finally,
These equations specify how the total energy in the laboratory frame is distributed between
the two particles after the collision. Note that
the energy distribution in the laboratory frame is different before and after the collision.
Equations (371)-(377), and some simple trigonometry, yield
 |
(383) |
and
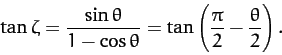 |
(384) |
The last equation implies that
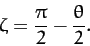 |
(385) |
Differentiating Equation (383) with respect to  , we obtain
, we obtain
 |
(386) |
Thus, 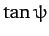 attains an extreme value, which can be shown to correspond to a maximum
possible value of
attains an extreme value, which can be shown to correspond to a maximum
possible value of 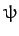 , when the numerator of the above expression is zero:
i.e., when
, when the numerator of the above expression is zero:
i.e., when
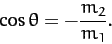 |
(387) |
Note that it is only possible to solve the above equation when 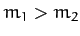 .
If this is the case then Equation (383) yields
.
If this is the case then Equation (383) yields
 |
(388) |
which reduces to
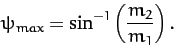 |
(389) |
Hence, we conclude that when 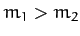 there is a maximum possible
value of the scattering angle,
there is a maximum possible
value of the scattering angle, 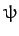 , in the laboratory frame. This maximum
value is always less than
, in the laboratory frame. This maximum
value is always less than 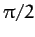 , which implies that there is
no backward scattering (i.e.,
, which implies that there is
no backward scattering (i.e., 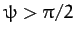 ) at all when
) at all when 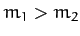 . For the special case when
. For the special case when
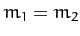 , the maximum scattering angle is
, the maximum scattering angle is 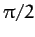 . However, for
. However, for
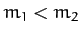 there is no maximum value, and the scattering angle in the laboratory frame can thus
range all the way to
there is no maximum value, and the scattering angle in the laboratory frame can thus
range all the way to  .
.
Equations (378)-(385) enable us to relate the
particle energies and scattering angles in the laboratory frame to those
in the center of mass frame. In general, these relationships are fairly complicated.
However, there are two special cases in which the relationships become
much simpler.
The first special case is when 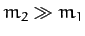 . In this limit, it is easily seen
from Equations (378)-(385) that the second mass is stationary
both before and after the collision, and that the center of mass frame
coincides with the laboratory frame (since the energies and
scattering angles in the two frames are the same). Hence, the simple analysis
outlined in Section 6.4 is applicable in this case.
. In this limit, it is easily seen
from Equations (378)-(385) that the second mass is stationary
both before and after the collision, and that the center of mass frame
coincides with the laboratory frame (since the energies and
scattering angles in the two frames are the same). Hence, the simple analysis
outlined in Section 6.4 is applicable in this case.
The second special case is when 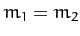 . In this case, Equation (383)
yields
. In this case, Equation (383)
yields
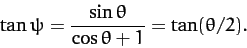 |
(390) |
Hence,
 |
(391) |
In other words, the scattering angle of the first particle in the laboratory
frame is half of the scattering angle in the center of mass frame.
The above equation can be combined with Equation (385) to
give
 |
(392) |
Thus, in the laboratory frame, the two particles move off at right-angles to one another after the collision. Equation (378)
yields
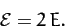 |
(393) |
In other words, the total energy in the laboratory frame is twice that
in the center of mass frame. According to Equations (379) and (380),
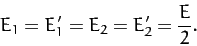 |
(394) |
Hence, the total energy in the center of mass frame is divided equally between the two particles. Finally, Equations (381) and (382)
give
Thus, in the laboratory frame, the unequal energy distribution between the two particles
after the collision is simply related to
the scattering angle 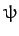 .
.
What is the angular distribution of scattered particles when a beam
of particles of the first type scatter off stationary particles of the second type?
Well, we can define a differential scattering cross-section,
 , in the
laboratory frame, where
, in the
laboratory frame, where
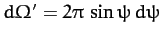 is an element of solid angle in
this frame. Thus,
is an element of solid angle in
this frame. Thus,
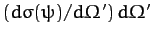 is the effective cross-sectional area in the laboratory frame
for scattering into the range of scattering angles
is the effective cross-sectional area in the laboratory frame
for scattering into the range of scattering angles 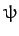 to
to 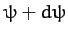 .
Likewise,
.
Likewise,
 is
the effective cross-sectional area in the center of mass frame for
scattering into the range of scattering angles
is
the effective cross-sectional area in the center of mass frame for
scattering into the range of scattering angles  to
to
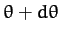 .
Note that
.
Note that
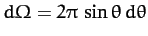 .
However, a cross-sectional area is not changed when we transform between
different inertial frames. Hence, we can write
.
However, a cross-sectional area is not changed when we transform between
different inertial frames. Hence, we can write
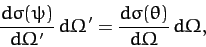 |
(397) |
provided that 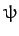 and
and  are related via Equation (383).
This equation can be rearranged to give
are related via Equation (383).
This equation can be rearranged to give
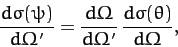 |
(398) |
or
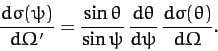 |
(399) |
The above equation allows us to relate the differential scattering cross-section
in the laboratory frame to that in the center of mass frame. In general, this
relationship is extremely complicated. However, for the special
case where the masses of the two types of particles are equal, we
have seen that  [see Equation (391)]. Hence, it follows from Equation (399)
that
[see Equation (391)]. Hence, it follows from Equation (399)
that
 |
(400) |
Let us now consider some specific examples. We saw earlier that, in the
center of mass frame, the
differential scattering cross-section for impenetrable spheres is [see Equation (356)]
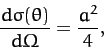 |
(401) |
where 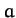 is the sum of the radii. According to Equation (400),
the differential scattering cross-section (for equal mass spheres) in the laboratory frame is
is the sum of the radii. According to Equation (400),
the differential scattering cross-section (for equal mass spheres) in the laboratory frame is
 |
(402) |
Note that this cross-section is negative for 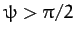 . This
just tells us that there is no scattering with scattering angles
greater than
. This
just tells us that there is no scattering with scattering angles
greater than 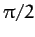 (i.e., there is no backward scattering).
Comparing Equations (401) and (402), we can see that
the scattering is isotropic in the center of mass frame, but appears
concentrated in the forward direction in the laboratory frame.
We can integrate Equation (402) over all solid angles to obtain the
total scattering cross-section in the laboratory frame. Note that we
only integrate over angular regions where the differential scattering
cross-section is positive. Doing this, we get
(i.e., there is no backward scattering).
Comparing Equations (401) and (402), we can see that
the scattering is isotropic in the center of mass frame, but appears
concentrated in the forward direction in the laboratory frame.
We can integrate Equation (402) over all solid angles to obtain the
total scattering cross-section in the laboratory frame. Note that we
only integrate over angular regions where the differential scattering
cross-section is positive. Doing this, we get
 |
(403) |
which is the same as the total scattering cross-section in the center of mass
frame [see Equation (357)]. This is a general result. The total scattering cross-section is
frame independent, since a cross-sectional area is not modified by
switching between different frames of reference.
As we have seen, the Rutherford scattering cross-section takes
the form [see Equation (367)]
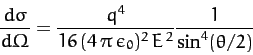 |
(404) |
in the center of mass frame.
It follows, from Equation (400), that the Rutherford scattering
cross-section (for equal mass particles) in the laboratory frame is written
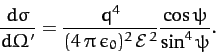 |
(405) |
Here, we have made use of the fact that
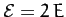 for equal
mass particles [see Equation (393)]. Note, again, that this cross-section is negative
for
for equal
mass particles [see Equation (393)]. Note, again, that this cross-section is negative
for 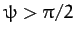 , indicating the absence of backward scattering.
, indicating the absence of backward scattering.



Next: Exercises
Up: Two-Body Dynamics
Previous: Scattering in the Center
Richard Fitzpatrick
2011-03-31
![]() before the collision, and velocity
before the collision, and velocity ![]() after the
collision. Likewise, the second particle has velocity
after the
collision. Likewise, the second particle has velocity ![]() before the
collision, and
before the
collision, and ![]() after the collision. We know that
after the collision. We know that
![]() with respect to
the center of mass frame. In the new reference frame, the first
particle has initial velocity
with respect to
the center of mass frame. In the new reference frame, the first
particle has initial velocity
![]() , and
final velocity
, and
final velocity
![]() . Furthermore, the second particle
is initially at rest, and has the final velocity
. Furthermore, the second particle
is initially at rest, and has the final velocity
![]() . The relationship between scattering in the center of mass frame
and scattering in the laboratory frame is illustrated in Figure 23.
. The relationship between scattering in the center of mass frame
and scattering in the laboratory frame is illustrated in Figure 23.
![]() . However, in the laboratory frame, the first and second particles
are scattered by the (generally different) angles
. However, in the laboratory frame, the first and second particles
are scattered by the (generally different) angles ![]() and
and ![]() ,
respectively.
,
respectively.
![]() - and
- and ![]() -axes, as indicated in Figure 23, it is easily
seen that the Cartesian components of the various velocity vectors in the
two frames of reference are:
-axes, as indicated in Figure 23, it is easily
seen that the Cartesian components of the various velocity vectors in the
two frames of reference are:
![]() be the total energy, let
be the total energy, let
![]() and
and
![]() be the kinetic energies of the first and second particles, respectively, before the collision, and let
be the kinetic energies of the first and second particles, respectively, before the collision, and let
![]() and
and
![]() be the kinetic energies of the first and second particles, respectively, after the collision. Of course,
be the kinetic energies of the first and second particles, respectively, after the collision. Of course,
![]() .
In the laboratory frame, let
.
In the laboratory frame, let ![]() be the total energy. This is, of course,
equal to the kinetic energy of the first particle before the collision. Likewise,
let
be the total energy. This is, of course,
equal to the kinetic energy of the first particle before the collision. Likewise,
let
![]() and
and
![]() be the kinetic energies of the first and second particles, respectively, after the collision. Of course,
be the kinetic energies of the first and second particles, respectively, after the collision. Of course,
![]() .
.
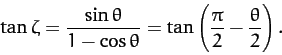


![]() . In this limit, it is easily seen
from Equations (378)-(385) that the second mass is stationary
both before and after the collision, and that the center of mass frame
coincides with the laboratory frame (since the energies and
scattering angles in the two frames are the same). Hence, the simple analysis
outlined in Section 6.4 is applicable in this case.
. In this limit, it is easily seen
from Equations (378)-(385) that the second mass is stationary
both before and after the collision, and that the center of mass frame
coincides with the laboratory frame (since the energies and
scattering angles in the two frames are the same). Hence, the simple analysis
outlined in Section 6.4 is applicable in this case.
![]() . In this case, Equation (383)
yields
. In this case, Equation (383)
yields

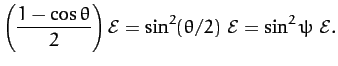
![]() , in the
laboratory frame, where
, in the
laboratory frame, where
![]() is an element of solid angle in
this frame. Thus,
is an element of solid angle in
this frame. Thus,
![]() is the effective cross-sectional area in the laboratory frame
for scattering into the range of scattering angles
is the effective cross-sectional area in the laboratory frame
for scattering into the range of scattering angles ![]() to
to ![]() .
Likewise,
.
Likewise,
![]() is
the effective cross-sectional area in the center of mass frame for
scattering into the range of scattering angles
is
the effective cross-sectional area in the center of mass frame for
scattering into the range of scattering angles ![]() to
to
![]() .
Note that
.
Note that
![]() .
However, a cross-sectional area is not changed when we transform between
different inertial frames. Hence, we can write
.
However, a cross-sectional area is not changed when we transform between
different inertial frames. Hence, we can write