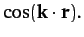Next: About this document ...
Up: Vector Algebra and Vector
Previous: Curvilinear Coordinates
- The position vectors of the four points
 ,
,  ,
,  , and
, and 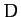 are
are 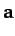 ,
, 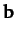 ,
,
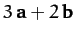 ,
and
,
and
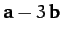 , respectively. Express
, respectively. Express
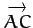 ,
,
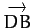 ,
,
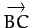 , and
, and
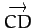 in terms of
in terms of 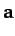 and
and 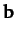 .
.
- Prove the trigonometric law of sines
using vector methods. Here, 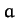 ,
, 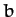 , and
, and 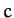 are the three
angles of a plane triangle, and
are the three
angles of a plane triangle, and 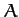 ,
, 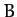 , and
, and 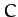 the lengths of the corresponding opposite sides.
the lengths of the corresponding opposite sides.
- Demonstrate using vectors that the diagonals of a parallelogram bisect one another. In addition, show that if the diagonals of a quadrilateral bisect one another then it is a parallelogram.
- From the inequality
deduce the triangle inequality
- Find the scalar product
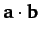 and the vector product
and the vector product
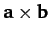 when
when
-
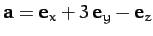 ,
,
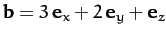 ,
,
-
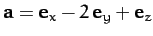 ,
,
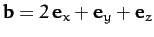 .
.
- Which of the following statements regarding the three general vectors
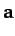 ,
, 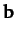 , and
, and 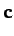 are true?
are true?
-
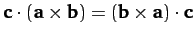 .
.
-
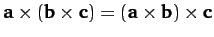 .
.
-
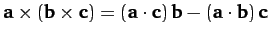 .
.
-
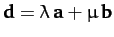 implies that
implies that
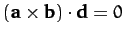 .
.
-
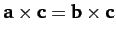 implies that
implies that
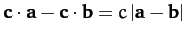 .
.
-
![$({\bf a}\times {\bf b})\times ({\bf c}\times {\bf b}) = [{\bf b}\cdot({\bf c}\times {\bf a})]\,{\bf b}$](img3524.png) .
.
- Prove that the length of the shortest straight-line from point
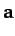 to the
straight-line joining points
to the
straight-line joining points 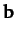 and
and 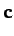 is
is
- Identify the following surfaces:
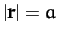 ,
,
-
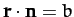 ,
,
-
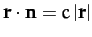 ,
,
-
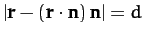 .
.
Here, 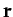 is the position vector,
is the position vector, 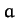 ,
, 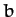 ,
, 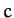 , and
, and 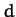 are positive
constants, and
are positive
constants, and 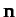 is a fixed unit vector.
is a fixed unit vector.
- Let
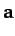 ,
, 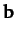 , and
, and 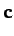 be coplanar vectors related via
be coplanar vectors related via
where 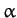 ,
, 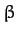 , and
, and 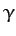 are not all zero. Show that the condition
for the points with position vectors
are not all zero. Show that the condition
for the points with position vectors 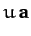 ,
, 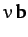 ,
and
,
and 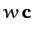 to be colinear is
to be colinear is
- If
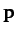 ,
, 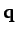 , and
, and 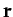 are any vectors, demonstrate that
are any vectors, demonstrate that
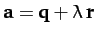 ,
,
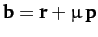 ,
and
,
and
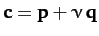 are coplanar provided that
are coplanar provided that
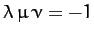 , where
, where 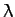 ,
, 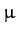 , and
, and 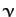 are scalars.
Show that this condition is satisfied when
are scalars.
Show that this condition is satisfied when 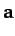 is perpendicular to
is perpendicular to 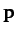 ,
, 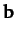 to
to 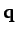 , and
, and 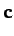 to
to 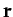 .
.
- The vectors
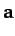 ,
, 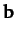 , and
, and 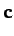 are non-coplanar, and
form a non-orthogonal vector base. The vectors
are non-coplanar, and
form a non-orthogonal vector base. The vectors 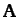 ,
, 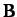 ,
and
,
and 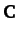 , defined by
, defined by
plus cyclic permutations, are said to be reciprocal vectors. Show that
plus cyclic permutations.
- In the notation of the previous question, demonstrate that the plane passing
through points
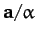 ,
, 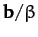 , and
, and
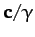 is normal to the direction of the vector
is normal to the direction of the vector
In addition, show that the perpendicular distance of the plane from the
origin is
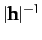 .
.
- Evaluate
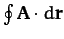 for
for
around the square whose sides are 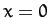 ,
,  ,
, 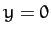 ,
, 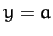 .
.
- Find the gradients of the following scalar functions of the position vector
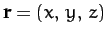 :
:
-
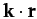 ,
,
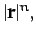
-
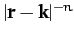 ,
,
-
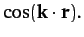
Here, 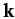 is a fixed vector.
is a fixed vector.



Next: About this document ...
Up: Vector Algebra and Vector
Previous: Curvilinear Coordinates
Richard Fitzpatrick
2011-03-31
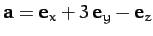 ,
,
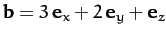 ,
,
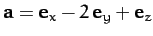 ,
,
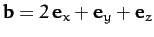 .
.
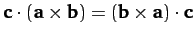 .
.
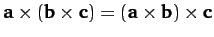 .
.
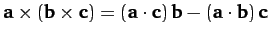 .
.
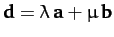 implies that
implies that
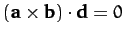 .
.
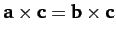 implies that
implies that
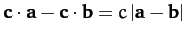 .
.
![$({\bf a}\times {\bf b})\times ({\bf c}\times {\bf b}) = [{\bf b}\cdot({\bf c}\times {\bf a})]\,{\bf b}$](img3524.png) .
.
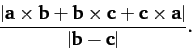
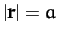 ,
,
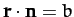 ,
,
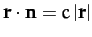 ,
,
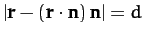 .
.
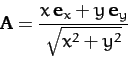
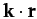 ,
,
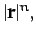
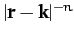 ,
,