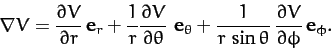Next: Exercises
Up: Vector Algebra and Vector
Previous: Grad Operator
Curvilinear Coordinates
In the cylindrical coordinate system, the Cartesian coordinates  and
and
 are replaced by
are replaced by
 and
and
 .
Here,
.
Here, 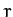 is the perpendicular distance from the
is the perpendicular distance from the  -axis, and
-axis, and  the angle subtended between the perpendicular radius vector and the
the angle subtended between the perpendicular radius vector and the  -axis--see
Figure A.113. A general vector
-axis--see
Figure A.113. A general vector 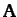 is thus written
is thus written
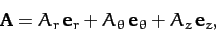 |
(1372) |
where
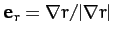 and
and
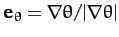 --see Figure A.113. Note that the unit vectors
--see Figure A.113. Note that the unit vectors
 ,
,
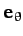 , and
, and 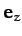 are mutually orthogonal.
Hence,
are mutually orthogonal.
Hence,
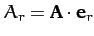 , etc. The
volume element in this coordinate system is
, etc. The
volume element in this coordinate system is
 .
Moreover, the gradient of a general scalar field
.
Moreover, the gradient of a general scalar field 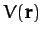 takes the form
takes the form
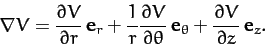 |
(1373) |
In the spherical coordinate system, the Cartesian coordinates
 ,
,  , and
, and  are replaced by
are replaced by
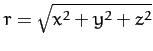 ,
,
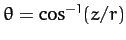 ,
and
,
and
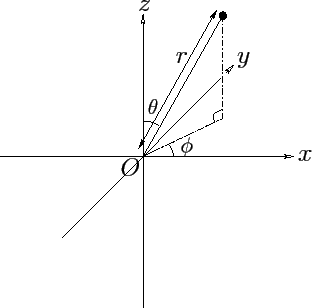
 . Here,
. Here, 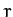 is the radial distance from the origin,
is the radial distance from the origin,
 the angle subtended between the radius vector and the
the angle subtended between the radius vector and the  -axis,
and
-axis,
and 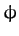 the angle subtended between the projection of the radius vector
onto the
the angle subtended between the projection of the radius vector
onto the  -
- plane and the
plane and the  -axis--see Figure A.114.
Note that
-axis--see Figure A.114.
Note that 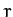 and
and  in the spherical system are not the same as their counterparts in the cylindrical system.
A general vector
in the spherical system are not the same as their counterparts in the cylindrical system.
A general vector 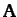 is written
is written
 |
(1374) |
where
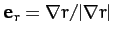 ,
,
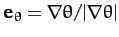 , and
, and
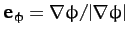 . The unit
vectors
. The unit
vectors  ,
,
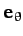 , and
, and 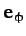 are mutually
orthogonal. Hence,
are mutually
orthogonal. Hence,
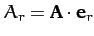 , etc.
The
volume element in this coordinate system is
, etc.
The
volume element in this coordinate system is
 .
Moreover, the gradient of a general scalar field
.
Moreover, the gradient of a general scalar field 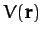 takes the form
takes the form
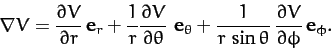 |
(1375) |
Figure A.114:
Spherical polar coordinates.
 |



Next: Exercises
Up: Vector Algebra and Vector
Previous: Grad Operator
Richard Fitzpatrick
2011-03-31
 and
and
![]() ,
, ![]() , and
, and ![]() are replaced by
are replaced by
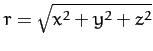 ,
,
![]() ,
and
,
and
![]() . Here,
. Here, ![]() is the radial distance from the origin,
is the radial distance from the origin,
![]() the angle subtended between the radius vector and the
the angle subtended between the radius vector and the ![]() -axis,
and
-axis,
and ![]() the angle subtended between the projection of the radius vector
onto the
the angle subtended between the projection of the radius vector
onto the ![]() -
-![]() plane and the
plane and the ![]() -axis--see Figure A.114.
Note that
-axis--see Figure A.114.
Note that ![]() and
and ![]() in the spherical system are not the same as their counterparts in the cylindrical system.
A general vector
in the spherical system are not the same as their counterparts in the cylindrical system.
A general vector ![]() is written
is written