


Next: Axially Symmetric Mass Distributions
Up: Gravitational Potential Theory
Previous: Introduction
Consider two point masses, 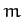 and
and 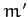 , located at position vectors
, located at position vectors
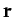 and
and 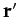 , respectively. According to Section 5.3,
the acceleration
, respectively. According to Section 5.3,
the acceleration 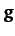 of mass
of mass 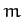 due to the gravitational force exerted on it by mass
due to the gravitational force exerted on it by mass 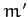 takes the form
takes the form
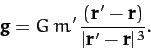 |
(861) |
Now, the  -component of this acceleration is written
-component of this acceleration is written
![\begin{displaymath}
g_x = G\,m'\,\frac{(x'-x)}{[(x'-x)^2+(y'-y)^2+(z'-z)^2]^{\,3/2}},
\end{displaymath}](img2052.png) |
(862) |
where
 and
and
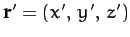 .
However, as is
easily demonstrated,
.
However, as is
easily demonstrated,
![$\displaystyle \frac{(x'-x)}{[(x'-x)^2+(y'-y)^2+(z'-z)^2]^{\,3/2}}\equiv
\frac{...
...tial}{\partial x}\!\left(\frac{1}{[(x'-x)^2+(y'-y)^2+(z'-z)^2]^{\,1/2}}\right).$](img2055.png) |
|
|
|
| |
|
|
(863) |
Hence,
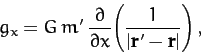 |
(864) |
with analogous expressions for 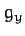 and
and 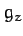 . It follows that
. It follows that
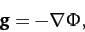 |
(865) |
where
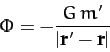 |
(866) |
is termed the gravitational potential. Of course,
we can only write 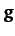 in the form (865) because gravity
is a conservative force--see Chapter 2.
Note that gravitational potential,
in the form (865) because gravity
is a conservative force--see Chapter 2.
Note that gravitational potential, 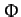 , is
directly related to gravitational potential energy,
, is
directly related to gravitational potential energy, 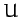 . In fact, the
potential energy of mass
. In fact, the
potential energy of mass 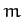 is
is
 .
.
Now, it is well-known that gravity is a superposable force. In other
words, the gravitational force exerted on some test mass by a collection
of point masses is simply the sum of the forces exerted on the test mass
by each point mass taken in isolation. It follows that
the gravitational potential generated by a collection of point masses
at a certain location in space is the sum of the potentials generated at that
location by each point mass taken in isolation. Hence, using Equation (866), if there are 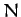 point masses,
point masses, 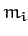 (for
(for  ), located at position vectors
), located at position vectors 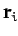 ,
then the gravitational potential generated at position vector
,
then the gravitational potential generated at position vector 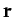 is simply
is simply
 |
(867) |
Suppose, finally, that, instead of having a collection of point masses, we have
a continuous mass distribution. In other words, let the mass at position
vector 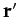 be
be
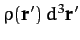 , where
, where
 is the local mass density, and
is the local mass density, and 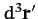 a volume element.
Summing over all space, and taking the limit
a volume element.
Summing over all space, and taking the limit
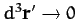 ,
Equation (867) yields
,
Equation (867) yields
 |
(868) |
where the integral is taken over all space.
This is the general expression for the gravitational potential, 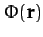 , generated by
a continuous mass distribution,
, generated by
a continuous mass distribution, 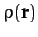 .
.



Next: Axially Symmetric Mass Distributions
Up: Gravitational Potential Theory
Previous: Introduction
Richard Fitzpatrick
2011-03-31
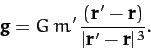
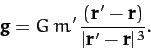
![\begin{displaymath}
g_x = G\,m'\,\frac{(x'-x)}{[(x'-x)^2+(y'-y)^2+(z'-z)^2]^{\,3/2}},
\end{displaymath}](img2052.png)
![$\displaystyle \frac{(x'-x)}{[(x'-x)^2+(y'-y)^2+(z'-z)^2]^{\,3/2}}\equiv
\frac{...
...tial}{\partial x}\!\left(\frac{1}{[(x'-x)^2+(y'-y)^2+(z'-z)^2]^{\,1/2}}\right).$](img2055.png)
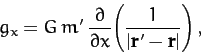
![]() point masses,
point masses, ![]() (for
(for ![]() ), located at position vectors
), located at position vectors ![]() ,
then the gravitational potential generated at position vector
,
then the gravitational potential generated at position vector ![]() is simply
is simply
![]() be
be
![]() , where
, where
![]() is the local mass density, and
is the local mass density, and ![]() a volume element.
Summing over all space, and taking the limit
a volume element.
Summing over all space, and taking the limit
![]() ,
Equation (867) yields
,
Equation (867) yields