


Next: Rigid Body Rotation
Up: Rotating Reference Frames
Previous: Foucault Pendulum
- A pebble is dropped down an elevator shaft in the Empire State
Building (
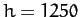 ft, latitude
ft, latitude  N). Find the pebble's horizontal deflection (magnitude and direction)
due to the Coriolis force at the bottom of the shaft. Neglect air resistance.
N). Find the pebble's horizontal deflection (magnitude and direction)
due to the Coriolis force at the bottom of the shaft. Neglect air resistance.
- If a bullet is fired due east, at an elevation angle
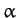 , from a point
on the Earth whose latitude is
, from a point
on the Earth whose latitude is 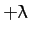 show that it will strike the
Earth with a lateral deflection
show that it will strike the
Earth with a lateral deflection
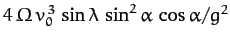 .
Is the deflection northward or southward?
Here,
.
Is the deflection northward or southward?
Here,  is the Earth's angular velocity,
is the Earth's angular velocity, 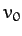 is the bullet's initial speed, and
is the bullet's initial speed, and
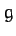 is the acceleration due to gravity. Neglect air resistance.
is the acceleration due to gravity. Neglect air resistance.
- A particle is thrown vertically with initial speed
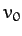 , reaches
a maximum height, and falls back to the ground. Show that the horizontal Coriolis
deflection of the particle when it returns to the ground is opposite in direction,
and four times greater in magnitude, than the Coriolis deflection when it
is dropped at rest from the same maximum height. Neglect air resistance.
, reaches
a maximum height, and falls back to the ground. Show that the horizontal Coriolis
deflection of the particle when it returns to the ground is opposite in direction,
and four times greater in magnitude, than the Coriolis deflection when it
is dropped at rest from the same maximum height. Neglect air resistance.
- The surface of the Diskworld is a disk which
rotates (counter-clockwise looking down) with angular frequency
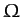 about a perpendicular axis passing through
its center. Diskworld gravitational acceleration is of magnitude
about a perpendicular axis passing through
its center. Diskworld gravitational acceleration is of magnitude
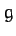 , and is everywhere directed normal to the disk.
A projectile is launched from the surface of the disk at a point whose radial distance from the axis of rotation is
, and is everywhere directed normal to the disk.
A projectile is launched from the surface of the disk at a point whose radial distance from the axis of rotation is 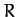 .
The initial velocity of the projectile (in a co-rotating frame) is of magnitude
.
The initial velocity of the projectile (in a co-rotating frame) is of magnitude 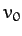 , is directly radially
outwards, and is inclined at an angle
, is directly radially
outwards, and is inclined at an angle 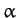 to the horizontal.
What are the radial and tangential displacements of the impact point
from that calculated by neglecting the centrifugal and Coriolis forces?
Neglect air resistance. You may assume that the displacements are small
compared to both
to the horizontal.
What are the radial and tangential displacements of the impact point
from that calculated by neglecting the centrifugal and Coriolis forces?
Neglect air resistance. You may assume that the displacements are small
compared to both 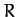 and the horizontal range of the projectile.
and the horizontal range of the projectile.
- Demonstrate that the Coriolis force causes conical pendulums to
rotate clockwise and counter-clockwise with slightly different angular frequencies. What
is the frequency difference as a function of terrestrial latitude?
- A satellite is in a circular orbit of radius
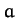 about the Earth.
Let us define a set of co-moving Cartesian coordinates, centered on the satellite, such that
the
about the Earth.
Let us define a set of co-moving Cartesian coordinates, centered on the satellite, such that
the 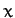 -axis always points toward the center of the Earth, the
-axis always points toward the center of the Earth, the 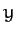 -axis in the
direction of the satellite's orbital motion, and the
-axis in the
direction of the satellite's orbital motion, and the 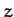 -axis in the direction
of the satellite's orbital angular velocity,
-axis in the direction
of the satellite's orbital angular velocity,
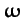 . Demonstrate that the
equation of motion of a small mass in orbit about the satellite are
. Demonstrate that the
equation of motion of a small mass in orbit about the satellite are
assuming that 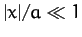 and
and 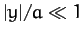 . You may neglect the gravitational
attraction between the satellite and the mass.
Show that the mass
executes a retrograde (i.e., in the opposite sense to the
satellite's orbital rotation) elliptical orbit about the satellite whose
period matches that of the satellite's orbit, and whose major and minor axes
are in the ratio
. You may neglect the gravitational
attraction between the satellite and the mass.
Show that the mass
executes a retrograde (i.e., in the opposite sense to the
satellite's orbital rotation) elliptical orbit about the satellite whose
period matches that of the satellite's orbit, and whose major and minor axes
are in the ratio 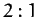 , and are aligned along the
, and are aligned along the 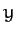 - and
- and 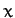 -axes,
respectively.
-axes,
respectively.



Next: Rigid Body Rotation
Up: Rotating Reference Frames
Previous: Foucault Pendulum
Richard Fitzpatrick
2011-03-31