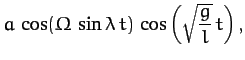Next: Exercises
Up: Rotating Reference Frames
Previous: Coriolis Force
Consider a pendulum consisting of a compact mass  suspended from a light cable of length
suspended from a light cable of length 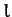 in such
a manner that the pendulum is free to oscillate in any plane whose
normal is parallel to the Earth's surface. The mass is
subject to three forces: first, the force of gravity
in such
a manner that the pendulum is free to oscillate in any plane whose
normal is parallel to the Earth's surface. The mass is
subject to three forces: first, the force of gravity 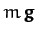 , which
is directed vertically downward (we are again ignoring centrifugal
acceleration); second, the tension
, which
is directed vertically downward (we are again ignoring centrifugal
acceleration); second, the tension 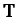 in the cable, which is directed upward
along the cable; and, third, the Coriolis force. It follows that the
apparent equation of motion of the mass, in a frame of
reference which co-rotates with the Earth, is [see Equation (414)]
in the cable, which is directed upward
along the cable; and, third, the Coriolis force. It follows that the
apparent equation of motion of the mass, in a frame of
reference which co-rotates with the Earth, is [see Equation (414)]
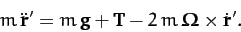 |
(438) |
Let us define our usual Cartesian coordinates (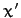 ,
, ,
,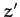 ), and
let the origin of our coordinate system correspond to the equilibrium position
of the mass. If the pendulum cable is deflected from the downward vertical by a small angle
), and
let the origin of our coordinate system correspond to the equilibrium position
of the mass. If the pendulum cable is deflected from the downward vertical by a small angle
 then it is easily seen that
then it is easily seen that
 ,
,
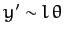 ,
and
,
and
 . In other words, the change in height
of the mass,
. In other words, the change in height
of the mass, 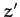 , is negligible compared to its horizontal displacement.
Hence, we can write
, is negligible compared to its horizontal displacement.
Hence, we can write  , provided that
, provided that 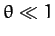 . The
tension
. The
tension 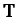 has the vertical component
has the vertical component
 ,
and the horizontal component
,
and the horizontal component
 , since
, since
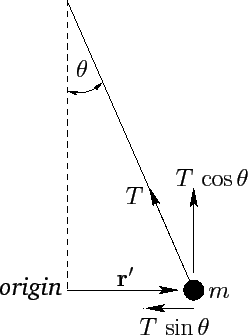
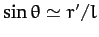 --see Figure 27. Hence, the
Cartesian equations of motion of the mass are written [cf., Equations (424)-(426)]
--see Figure 27. Hence, the
Cartesian equations of motion of the mass are written [cf., Equations (424)-(426)]
To lowest order in  (i.e., neglecting
(i.e., neglecting  ), the final equation, which is just vertical force balance, yields
), the final equation, which is just vertical force balance, yields 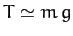 .
Hence, Equations (439) and (440) reduce to
.
Hence, Equations (439) and (440) reduce to
Figure 27:
The Foucault pendulum.
 |
Let
 |
(444) |
Equations (442) and (443) can be combined to give a single complex
equation for  :
:
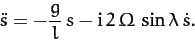 |
(445) |
Let us look for a sinusoidally oscillating solution of the form
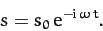 |
(446) |
Here, 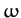 is the (real) angular frequency of oscillation, and
is the (real) angular frequency of oscillation, and  is an arbitrary complex constant. Equations (445) and (446)
yield the following quadratic equation for
is an arbitrary complex constant. Equations (445) and (446)
yield the following quadratic equation for 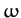 :
:
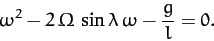 |
(447) |
The solutions are approximately
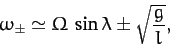 |
(448) |
where we have neglected terms involving
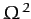 .
Hence, the general solution of (446) takes the form
.
Hence, the general solution of (446) takes the form
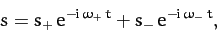 |
(449) |
where  and
and 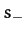 are two arbitrary complex constants.
are two arbitrary complex constants.
Making the specific choice 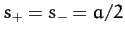 , where
, where 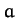 is real, the
above solution reduces to
is real, the
above solution reduces to
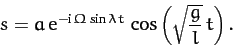 |
(450) |
Now, it is clear from Equation (444) that 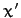 and
and  are the real and imaginary
parts of
are the real and imaginary
parts of 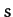 , respectively. Thus, it follows from the above that
, respectively. Thus, it follows from the above that
These equations describe sinusoidal oscillations, in a plane whose normal
is parallel to the Earth's surface, at the standard pendulum frequency 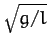 .
The Coriolis force, however, causes the plane of oscillation to slowly precess at the
angular frequency
.
The Coriolis force, however, causes the plane of oscillation to slowly precess at the
angular frequency
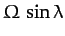 . The period of the
precession is
. The period of the
precession is
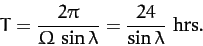 |
(453) |
For example, according to the above equations, the pendulum oscillates
in the 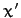 -direction (i.e., north/south) at
-direction (i.e., north/south) at 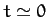 , in the
, in the  -direction
(i.e., east/west) at
-direction
(i.e., east/west) at  , in the
, in the 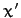 -direction again at
-direction again at 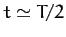 , etc. The precession is clockwise (looking from above)
in the northern hemisphere, and counter-clockwise
in the southern
hemisphere.
, etc. The precession is clockwise (looking from above)
in the northern hemisphere, and counter-clockwise
in the southern
hemisphere.
The precession of the plane of oscillation of a pendulum, due to
the Coriolis force, is used in many museums and observatories to
demonstrate that the Earth is rotating. This method of making the
Earth's rotation manifest was first devised by Foucault in 1851.



Next: Exercises
Up: Rotating Reference Frames
Previous: Coriolis Force
Richard Fitzpatrick
2011-03-31
![]() ,
,![]() ,
,![]() ), and
let the origin of our coordinate system correspond to the equilibrium position
of the mass. If the pendulum cable is deflected from the downward vertical by a small angle
), and
let the origin of our coordinate system correspond to the equilibrium position
of the mass. If the pendulum cable is deflected from the downward vertical by a small angle
![]() then it is easily seen that
then it is easily seen that
![]() ,
,
![]() ,
and
,
and
![]() . In other words, the change in height
of the mass,
. In other words, the change in height
of the mass, ![]() , is negligible compared to its horizontal displacement.
Hence, we can write
, is negligible compared to its horizontal displacement.
Hence, we can write ![]() , provided that
, provided that ![]() . The
tension
. The
tension ![]() has the vertical component
has the vertical component
![]() ,
and the horizontal component
,
and the horizontal component
![]() , since
, since
![]() --see Figure 27. Hence, the
Cartesian equations of motion of the mass are written [cf., Equations (424)-(426)]
--see Figure 27. Hence, the
Cartesian equations of motion of the mass are written [cf., Equations (424)-(426)]
![]() , where
, where ![]() is real, the
above solution reduces to
is real, the
above solution reduces to