


Next: Charged Particle Motion in
Up: Multi-Dimensional Motion
Previous: Motion in a Two-Dimensional
Suppose that a
projectile of mass 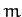 is launched, at
is launched, at  , from ground level (in a flat plain), making an angle
, from ground level (in a flat plain), making an angle 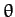 to the horizontal. Suppose, further, that, in addition
to the force of gravity, the projectile is subject to an air resistance
force which acts in the opposite direction to its instantaneous
direction of motion, and whose magnitude is directly proportional to its instantaneous speed. This is not a particularly accurate model
of the drag force due to air resistance (the magnitude of the drag force is typically proportion
to the square of the speed--see Section 3.3), but it does lead to
tractable equations of motion. Hence, by using this model we can, at least,
get some idea of how air resistance modifies projectile trajectories.
to the horizontal. Suppose, further, that, in addition
to the force of gravity, the projectile is subject to an air resistance
force which acts in the opposite direction to its instantaneous
direction of motion, and whose magnitude is directly proportional to its instantaneous speed. This is not a particularly accurate model
of the drag force due to air resistance (the magnitude of the drag force is typically proportion
to the square of the speed--see Section 3.3), but it does lead to
tractable equations of motion. Hence, by using this model we can, at least,
get some idea of how air resistance modifies projectile trajectories.
Let us adopt a Cartesian coordinate system whose origin coincides with the launch point, and whose 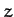 -axis
points vertically upward. Let the initial velocity of the projectile
lie in the
-axis
points vertically upward. Let the initial velocity of the projectile
lie in the  -
-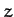 plane. Note that, since neither gravity nor the drag force
cause the projectile to move out of the
plane. Note that, since neither gravity nor the drag force
cause the projectile to move out of the  -
-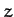 plane,
we can effectively ignore the
plane,
we can effectively ignore the 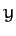 coordinate in this problem.
coordinate in this problem.
The equation of motion of our projectile is written
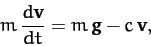 |
(175) |
where
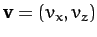 is the projectile velocity,
is the projectile velocity,
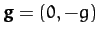 the acceleration due to gravity, and
the acceleration due to gravity, and
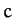 a positive constant. In component form, the
above equation becomes
a positive constant. In component form, the
above equation becomes
Here, 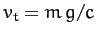 is the terminal velocity: i.e., the
velocity at which the drag force balances the gravitational force (for a
projectile falling vertically downward).
is the terminal velocity: i.e., the
velocity at which the drag force balances the gravitational force (for a
projectile falling vertically downward).
Integrating Equation (176), we obtain
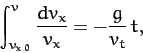 |
(178) |
where
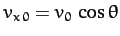 is the
is the  -component of the
launch velocity.
Hence,
-component of the
launch velocity.
Hence,
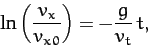 |
(179) |
or
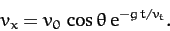 |
(180) |
It is clear, from the above equation, that air drag causes the projectile's horizontal
velocity, which would otherwise be constant, to decay exponentially on a time-scale of order 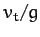 .
.
Integrating Equation (177), we get
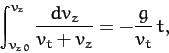 |
(181) |
where
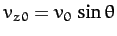 is the
is the 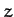 -component of the launch velocity. Hence,
-component of the launch velocity. Hence,
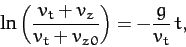 |
(182) |
or
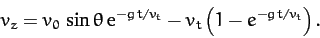 |
(183) |
It thus follows, from Equations (180) and (183), that if the
projectile stays in the air much longer than a time of order 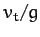 then
it ends up falling vertically downward at the terminal velocity,
then
it ends up falling vertically downward at the terminal velocity, 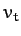 , irrespective
of its initial launch angle.
, irrespective
of its initial launch angle.
Integration of (180) yields
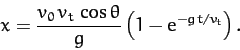 |
(184) |
In the limit 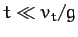 , the above equation reduces to
, the above equation reduces to
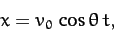 |
(185) |
which is the standard result in the absence of air drag.
In the opposite limit, 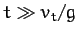 , we get
, we get
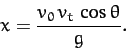 |
(186) |
The above expression clearly sets an effective upper limit on how far the
projectile can travel in the horizontal direction.
Integration of (183) gives
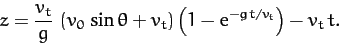 |
(187) |
In the limit 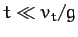 , this equation reduces to
, this equation reduces to
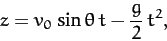 |
(188) |
which is the standard result in the absence of air drag. In the opposite
limit, 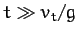 , we get
, we get
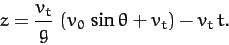 |
(189) |
Incidentally, the above analysis implies that air resistance
only starts to have an appreciable effect on the trajectory after
the projectile has been in the air a time of order 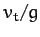 .
.
It is clear, from the previous two equations, that the time
of flight of the projectile (i.e., the time at which  , excluding the
trivial result
, excluding the
trivial result  ) is
) is
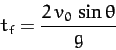 |
(190) |
when 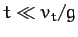 , which implies that
, which implies that
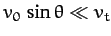 ,
and
,
and
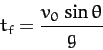 |
(191) |
when 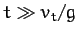 , which implies that
, which implies that
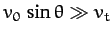 (i.e., the vertical component of the
launch velocity is much greater than the terminal velocity).
It thus follows, from Equations (185) and (186), that
the horizontal range [i.e.,
(i.e., the vertical component of the
launch velocity is much greater than the terminal velocity).
It thus follows, from Equations (185) and (186), that
the horizontal range [i.e., 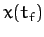 ] of the projectile
is
] of the projectile
is
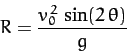 |
(192) |
when
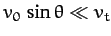 , and
, and
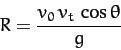 |
(193) |
when
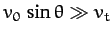 .
Equation (192) is, of course, the standard result without
air resistance. This result implies that, in the absence of air resistance, the maximum horizontal range,
.
Equation (192) is, of course, the standard result without
air resistance. This result implies that, in the absence of air resistance, the maximum horizontal range, 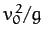 ,
is achieved when the launch angle
,
is achieved when the launch angle 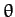 takes the value
takes the value 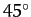 .
On the other hand, Equation (193) implies that, in the presence of
air resistance, the maximum horizontal
range,
.
On the other hand, Equation (193) implies that, in the presence of
air resistance, the maximum horizontal
range, 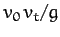 , is achieved when
, is achieved when 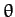 is made as small
as possible. However,
is made as small
as possible. However, 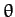 cannot be made too small, since
expression (193) is only valid when
cannot be made too small, since
expression (193) is only valid when
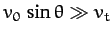 .
In fact, assuming that
.
In fact, assuming that 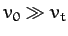 , the maximum horizontal
range,
, the maximum horizontal
range, 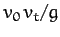 , is achieved when
, is achieved when
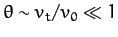 . We thus
conclude that if air resistance is significant then it causes the horizontal range of the
projectile to scale linearly, rather than quadratically, with the
launch velocity,
. We thus
conclude that if air resistance is significant then it causes the horizontal range of the
projectile to scale linearly, rather than quadratically, with the
launch velocity, 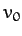 . Moreover, the maximum horizontal range is achieved
with a launch angle which is much shallower than the standard
result,
. Moreover, the maximum horizontal range is achieved
with a launch angle which is much shallower than the standard
result, 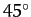 .
.
Figure 11:
Projectile trajectories in the presence of air resistance.
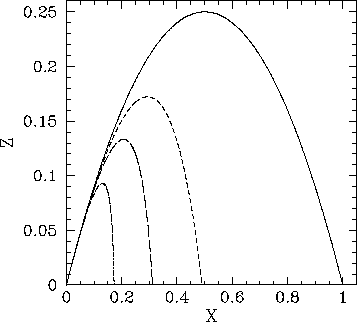 |
Figure 11 shows some example trajectories calculated, from the above model, with the same launch
angle, 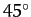 , but with different values of the ratio
, but with different values of the ratio 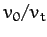 . Here,
. Here,
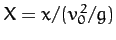 and
and
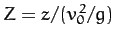 . The solid, short-dashed,
long-dashed, and dot-dashed curves correspond to
. The solid, short-dashed,
long-dashed, and dot-dashed curves correspond to 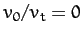 ,
, 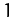 ,
, 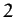 ,
and
,
and 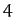 , respectively. It can be seen that as the air resistance strength
increases (i.e., as
, respectively. It can be seen that as the air resistance strength
increases (i.e., as 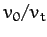 increases), the range of the
projectile decreases. Furthermore, there is always an initial time interval
during which the trajectory is identical to that calculated in the absence
of air resistance (i.e.,
increases), the range of the
projectile decreases. Furthermore, there is always an initial time interval
during which the trajectory is identical to that calculated in the absence
of air resistance (i.e., 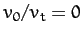 ). Finally, in the presence of
air resistance, the projectile tends to fall more steeply than it rises.
Indeed, in the presence of strong air resistance (i.e.,
). Finally, in the presence of
air resistance, the projectile tends to fall more steeply than it rises.
Indeed, in the presence of strong air resistance (i.e., 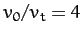 ), the projectile falls almost
vertically.
), the projectile falls almost
vertically.



Next: Charged Particle Motion in
Up: Multi-Dimensional Motion
Previous: Motion in a Two-Dimensional
Richard Fitzpatrick
2011-03-31
![]() -axis
points vertically upward. Let the initial velocity of the projectile
lie in the
-axis
points vertically upward. Let the initial velocity of the projectile
lie in the ![]() -
-![]() plane. Note that, since neither gravity nor the drag force
cause the projectile to move out of the
plane. Note that, since neither gravity nor the drag force
cause the projectile to move out of the ![]() -
-![]() plane,
we can effectively ignore the
plane,
we can effectively ignore the ![]() coordinate in this problem.
coordinate in this problem.
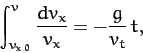
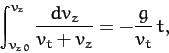
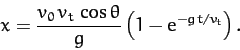
![]() , excluding the
trivial result
, excluding the
trivial result ![]() ) is
) is
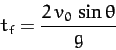
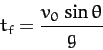
![]() , but with different values of the ratio
, but with different values of the ratio ![]() . Here,
. Here,
![]() and
and
![]() . The solid, short-dashed,
long-dashed, and dot-dashed curves correspond to
. The solid, short-dashed,
long-dashed, and dot-dashed curves correspond to ![]() ,
, ![]() ,
, ![]() ,
and
,
and ![]() , respectively. It can be seen that as the air resistance strength
increases (i.e., as
, respectively. It can be seen that as the air resistance strength
increases (i.e., as ![]() increases), the range of the
projectile decreases. Furthermore, there is always an initial time interval
during which the trajectory is identical to that calculated in the absence
of air resistance (i.e.,
increases), the range of the
projectile decreases. Furthermore, there is always an initial time interval
during which the trajectory is identical to that calculated in the absence
of air resistance (i.e., ![]() ). Finally, in the presence of
air resistance, the projectile tends to fall more steeply than it rises.
Indeed, in the presence of strong air resistance (i.e.,
). Finally, in the presence of
air resistance, the projectile tends to fall more steeply than it rises.
Indeed, in the presence of strong air resistance (i.e., ![]() ), the projectile falls almost
vertically.
), the projectile falls almost
vertically.