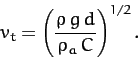Next: Simple Harmonic Motion
Up: One-Dimensional Motion
Previous: Motion in a General
Velocity Dependent Forces
Consider a particle of mass  moving in one dimension under the
action of a force,
moving in one dimension under the
action of a force, 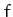 , which is a function of the particle's speed,
, which is a function of the particle's speed, 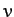 , but not
of its displacement,
, but not
of its displacement, 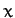 . Note that such a force is intrinsically non-conservative [since it clearly cannot be expressed as minus the gradient of
some potential function,
. Note that such a force is intrinsically non-conservative [since it clearly cannot be expressed as minus the gradient of
some potential function, 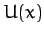 ].
Now, the particle's equation of motion is written
].
Now, the particle's equation of motion is written
 |
(56) |
Integrating this equation, we obtain
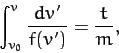 |
(57) |
where 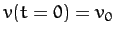 . In principle, the above equation can be solved to
give
. In principle, the above equation can be solved to
give  . The equation of motion is also written
. The equation of motion is also written
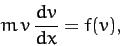 |
(58) |
since 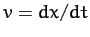 . Integrating this equation, we obtain
. Integrating this equation, we obtain
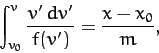 |
(59) |
where  . In principle, the above equation
can be solved to give
. In principle, the above equation
can be solved to give 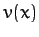 .
.
Let us now consider a specific example. Suppose that an object of mass  falls
vertically under gravity. Let
falls
vertically under gravity. Let 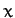 be the height through which the object
has fallen since
be the height through which the object
has fallen since  , at which time the object is assumed to be at rest. It follows that
, at which time the object is assumed to be at rest. It follows that
 . Suppose that, in addition to the force of gravity,
. Suppose that, in addition to the force of gravity, 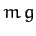 , where
, where 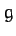 is the gravitational acceleration, our
object is subject to a retarding air resistance force which is proportional
to the square of its instantaneous velocity. The object's equation
of motion is thus
is the gravitational acceleration, our
object is subject to a retarding air resistance force which is proportional
to the square of its instantaneous velocity. The object's equation
of motion is thus
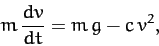 |
(60) |
where 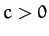 . This equation can be integrated to give
. This equation can be integrated to give
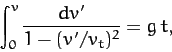 |
(61) |
where
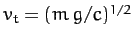 . Making a change of variable, we obtain
. Making a change of variable, we obtain
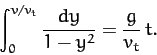 |
(62) |
The left-hand side of the above equation is now a standard integral, which can be solved to give
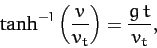 |
(63) |
or
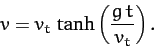 |
(64) |
Thus, when 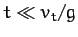 , we obtain the standard result
, we obtain the standard result 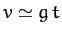 ,
since
,
since
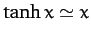 for
for 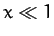 . However, when
. However, when 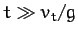 , we get
, we get
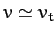 , since
, since
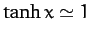 for
for 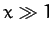 . It follows that
air resistance prevents the downward velocity of our object from
increasing indefinitely as it falls. Instead, at large times, the velocity asymptotically approaches
the so-called terminal velocity,
. It follows that
air resistance prevents the downward velocity of our object from
increasing indefinitely as it falls. Instead, at large times, the velocity asymptotically approaches
the so-called terminal velocity, 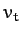 (at which the gravitational
and air resistance forces balance).
(at which the gravitational
and air resistance forces balance).
The equation of motion of our falling object is also written
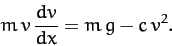 |
(65) |
This equation can be integrated to give
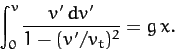 |
(66) |
Making a change of variable, we obtain
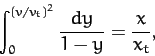 |
(67) |
where
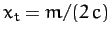 . The left-hand side of the above equation is now a standard integral, which can
be solved to give
. The left-hand side of the above equation is now a standard integral, which can
be solved to give
![\begin{displaymath}
-\ln\!\left[1-\left(\frac{v}{v_t}\right)^2\right] = \frac{x}{x_t},
\end{displaymath}](img273.png) |
(68) |
or
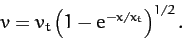 |
(69) |
It follows that our object needs to fall a distance
of order 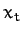 before it achieves its terminal velocity.
before it achieves its terminal velocity.
Incidentally, it is quite easy to account for an air resistance force
which scales as the square of projectile velocity. Let us imaging that
our projectile is moving sufficiently rapidly that air does not have enough
time to flow around it, and is instead simply knocked out of the way.
If our projectile has cross-sectional area 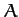 , perpendicular to the direction of its motion,
and is moving with speed
, perpendicular to the direction of its motion,
and is moving with speed 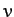 , then the mass of air that it knocks out of
its way per second is
, then the mass of air that it knocks out of
its way per second is 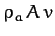 , where
, where 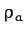 is the mass density
of air. Suppose that the air knocked out of the way is pushed in the direction
of the projectile's motion with a speed of order
is the mass density
of air. Suppose that the air knocked out of the way is pushed in the direction
of the projectile's motion with a speed of order 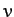 . It follows that the
air gains momentum per unit time
. It follows that the
air gains momentum per unit time
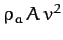 in the direction
of the projectile's motion. Hence, by Newton's third law, the projectile
loses the same momentum per unit time in the direction of its motion.
In other words, the projectile is subject to a drag force of magnitude
in the direction
of the projectile's motion. Hence, by Newton's third law, the projectile
loses the same momentum per unit time in the direction of its motion.
In other words, the projectile is subject to a drag force of magnitude
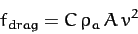 |
(70) |
acting in the opposite direction to its motion.
Here, 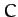 is an
is an  dimensionless constant, known as the
drag coefficient, which depends on the exact shape of the
projectile. Obviously, streamlined projectiles, such as arrows, have small drag coefficients,
whereas non-streamlined projectiles, such as bricks, have large drag
coefficients. From before, the terminal velocity of our projectile is
dimensionless constant, known as the
drag coefficient, which depends on the exact shape of the
projectile. Obviously, streamlined projectiles, such as arrows, have small drag coefficients,
whereas non-streamlined projectiles, such as bricks, have large drag
coefficients. From before, the terminal velocity of our projectile is
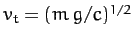 , where
, where  is its mass, and
is its mass, and
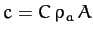 .
Writing
.
Writing
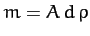 , where
, where  is the typical linear dimension
of the projectile, and
is the typical linear dimension
of the projectile, and 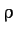 its mass density, we obtain
its mass density, we obtain
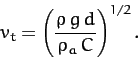 |
(71) |
The above expression tells us that large, dense, streamlined projectiles (e.g., medicine balls)
tend to have large terminal velocities, and small, rarefied, non-streamlined
projectiles (e.g., feathers) tend to have small terminal velocities. Hence, the former
type of projectile is relatively less affected by air resistance than the
latter.



Next: Simple Harmonic Motion
Up: One-Dimensional Motion
Previous: Motion in a General
Richard Fitzpatrick
2011-03-31
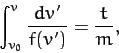
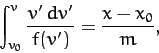
![]() falls
vertically under gravity. Let
falls
vertically under gravity. Let ![]() be the height through which the object
has fallen since
be the height through which the object
has fallen since ![]() , at which time the object is assumed to be at rest. It follows that
, at which time the object is assumed to be at rest. It follows that
![]() . Suppose that, in addition to the force of gravity,
. Suppose that, in addition to the force of gravity, ![]() , where
, where ![]() is the gravitational acceleration, our
object is subject to a retarding air resistance force which is proportional
to the square of its instantaneous velocity. The object's equation
of motion is thus
is the gravitational acceleration, our
object is subject to a retarding air resistance force which is proportional
to the square of its instantaneous velocity. The object's equation
of motion is thus
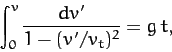
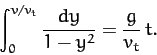
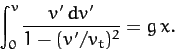
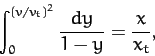
![\begin{displaymath}
-\ln\!\left[1-\left(\frac{v}{v_t}\right)^2\right] = \frac{x}{x_t},
\end{displaymath}](img273.png)
![]() , perpendicular to the direction of its motion,
and is moving with speed
, perpendicular to the direction of its motion,
and is moving with speed ![]() , then the mass of air that it knocks out of
its way per second is
, then the mass of air that it knocks out of
its way per second is ![]() , where
, where ![]() is the mass density
of air. Suppose that the air knocked out of the way is pushed in the direction
of the projectile's motion with a speed of order
is the mass density
of air. Suppose that the air knocked out of the way is pushed in the direction
of the projectile's motion with a speed of order ![]() . It follows that the
air gains momentum per unit time
. It follows that the
air gains momentum per unit time
![]() in the direction
of the projectile's motion. Hence, by Newton's third law, the projectile
loses the same momentum per unit time in the direction of its motion.
In other words, the projectile is subject to a drag force of magnitude
in the direction
of the projectile's motion. Hence, by Newton's third law, the projectile
loses the same momentum per unit time in the direction of its motion.
In other words, the projectile is subject to a drag force of magnitude