


Next: Normal Modes
Up: Coupled Oscillations
Previous: Stability Equations
More Matrix Eigenvalue Theory
Equation (785) takes the form of a matrix eigenvalue equation:
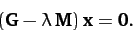 |
(786) |
Here, 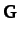 and
and 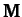 are both real symmetric matrices, whereas
are both real symmetric matrices, whereas
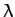 is termed the eigenvalue, and
is termed the eigenvalue, and 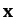 the associated eigenvector.
The above matrix equation is essentially a set of
the associated eigenvector.
The above matrix equation is essentially a set of  homogeneous simultaneous algebraic equations for the components of
homogeneous simultaneous algebraic equations for the components of 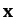 . As is well-known, a necessary condition for such a set of equations to possess a
non-trivial solution is that the determinant of the matrix must
be zero: i.e.,
. As is well-known, a necessary condition for such a set of equations to possess a
non-trivial solution is that the determinant of the matrix must
be zero: i.e.,
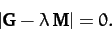 |
(787) |
The above formula reduces to an 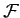 th-order polynomial equation
for
th-order polynomial equation
for 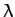 . Hence, we conclude that Equation (786) is satisfied
by
. Hence, we conclude that Equation (786) is satisfied
by 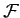 eigenvalues, and
eigenvalues, and 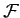 associated eigenvectors.
associated eigenvectors.
We can easily demonstrate that the eigenvalues are all real. Suppose
that 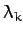 and
and 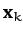 are the
are the  th eigenvalue and
eigenvector, respectively. Then we have
th eigenvalue and
eigenvector, respectively. Then we have
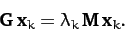 |
(788) |
Taking the transpose and complex conjugate of the above equation, and
right multiplying by 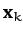 , we obtain
, we obtain
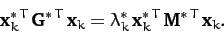 |
(789) |
Here, 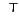 denotes a transpose, and
denotes a transpose, and 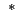 a complex conjugate.
However, since
a complex conjugate.
However, since 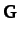 and
and 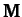 are both real symmetric
matrices, it follows that
are both real symmetric
matrices, it follows that
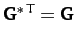 and
and
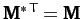 . Hence,
. Hence,
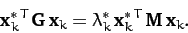 |
(790) |
Next, left multiplying Equation (788) by
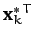 ,
we obtain
,
we obtain
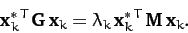 |
(791) |
Taking the difference between the above two expressions, we get
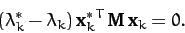 |
(792) |
Since
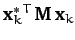 is not generally zero, except in the trivial case where
is not generally zero, except in the trivial case where
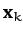 is a null vector, we conclude that
is a null vector, we conclude that
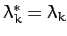 for all
for all  . In other words, the eigenvalues are all real. It immediately
follows that the eigenvectors can also be chosen to be all real.
. In other words, the eigenvalues are all real. It immediately
follows that the eigenvectors can also be chosen to be all real.
Consider two distinct eigenvalues, 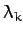 and
and 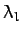 , with
the associated eigenvectors
, with
the associated eigenvectors 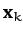 and
and  , respectively.
We have
, respectively.
We have
Right multiplying the transpose of Equation (793) by  ,
and left multiplying Equation (794) by
,
and left multiplying Equation (794) by 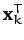 , we obtain
, we obtain
Taking the difference between the above two expressions, we get
 |
(797) |
Hence, we conclude that
 |
(798) |
provided
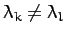 .
In other words, two eigenvectors corresponding to two different eigenvalues
are ``orthogonal'' to one another (in the sense specified in the above equation).
Moreover, it is easily demonstrated that different eigenvectors corresponding to the same
eigenvalue can be chosen in such a manner that they are also orthogonal to one another--see Section 8.5. Thus, we conclude
that all of the eigenvectors are mutually orthogonal. Since Equation (786) only specifies the directions, and not the lengths, of the
eigenvectors, we are free to normalize our eigenvectors such that
.
In other words, two eigenvectors corresponding to two different eigenvalues
are ``orthogonal'' to one another (in the sense specified in the above equation).
Moreover, it is easily demonstrated that different eigenvectors corresponding to the same
eigenvalue can be chosen in such a manner that they are also orthogonal to one another--see Section 8.5. Thus, we conclude
that all of the eigenvectors are mutually orthogonal. Since Equation (786) only specifies the directions, and not the lengths, of the
eigenvectors, we are free to normalize our eigenvectors such that
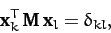 |
(799) |
where 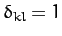 when
when  , and
, and 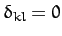 otherwise.
Note, finally, that since the
otherwise.
Note, finally, that since the 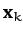 , for
, for 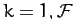 , are mutually orthogonal,
they are independent (i.e., one eigenvector cannot be expressed as a linear combination of the others), and completely span
, are mutually orthogonal,
they are independent (i.e., one eigenvector cannot be expressed as a linear combination of the others), and completely span 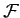 -dimensional vector space.
-dimensional vector space.



Next: Normal Modes
Up: Coupled Oscillations
Previous: Stability Equations
Richard Fitzpatrick
2011-03-31
![]() and
and ![]() are the
are the ![]() th eigenvalue and
eigenvector, respectively. Then we have
th eigenvalue and
eigenvector, respectively. Then we have
![]() and
and ![]() , with
the associated eigenvectors
, with
the associated eigenvectors ![]() and
and ![]() , respectively.
We have
, respectively.
We have