


Next: Principal Axes of Rotation
Up: Rigid Body Rotation
Previous: Rotational Kinetic Energy
Matrix Eigenvalue Theory
It is time to review a little matrix theory. Suppose that 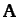 is
a real symmetric matrix of dimension
is
a real symmetric matrix of dimension  . If follows that
. If follows that
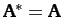 and
and
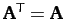 , where
, where 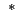 denotes a complex conjugate, and
denotes a complex conjugate, and 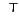 denotes a transpose.
Consider the matrix equation
denotes a transpose.
Consider the matrix equation
 |
(472) |
Any column vector 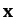 which satisfies the above equation is called
an eigenvector of
which satisfies the above equation is called
an eigenvector of 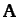 . Likewise, the associated number
. Likewise, the associated number 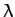 is called an eigenvalue of
is called an eigenvalue of 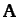 . Let us investigate the properties of the eigenvectors and eigenvalues of a real
symmetric matrix.
. Let us investigate the properties of the eigenvectors and eigenvalues of a real
symmetric matrix.
Equation (472) can be rearranged to give
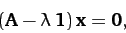 |
(473) |
where 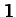 is the unit matrix. The above matrix equation is essentially a set of
is the unit matrix. The above matrix equation is essentially a set of  homogeneous
simultaneous algebraic equations for the
homogeneous
simultaneous algebraic equations for the  components of
components of 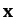 .
A well-known property of such a set of equations is that it only has a non-trivial
solution when the determinant of the associated matrix is set to zero.
Hence, a necessary condition for the above set of equations to have a non-trivial
solution is that
.
A well-known property of such a set of equations is that it only has a non-trivial
solution when the determinant of the associated matrix is set to zero.
Hence, a necessary condition for the above set of equations to have a non-trivial
solution is that
 |
(474) |
The above formula is essentially an  th-order polynomial equation
for
th-order polynomial equation
for 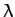 . We know that such an equation has
. We know that such an equation has  (possibly complex)
roots. Hence, we conclude that there are
(possibly complex)
roots. Hence, we conclude that there are  eigenvalues, and
eigenvalues, and  associated eigenvectors, of the
associated eigenvectors, of the  -dimensional matrix
-dimensional matrix 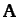 .
.
Let us now demonstrate that the  eigenvalues and eigenvectors of the real symmetric matrix
eigenvalues and eigenvectors of the real symmetric matrix
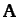 are all real. We have
are all real. We have
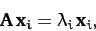 |
(475) |
and, taking the transpose and complex conjugate,
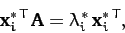 |
(476) |
where 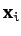 and
and  are the
are the 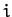 th eigenvector and eigenvalue
of
th eigenvector and eigenvalue
of 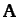 , respectively. Left multiplying Equation (475) by
, respectively. Left multiplying Equation (475) by
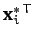 , we obtain
, we obtain
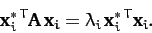 |
(477) |
Likewise, right multiplying (476) by 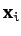 , we get
, we get
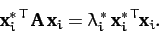 |
(478) |
The difference of the previous two equations yields
 |
(479) |
It follows that
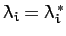 , since
, since
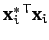 (which is
(which is
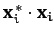 in vector notation) is positive definite. Hence,
in vector notation) is positive definite. Hence,  is real.
It immediately follows that
is real.
It immediately follows that 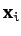 is real.
is real.
Next, let us show that two eigenvectors corresponding to two different eigenvalues are mutually orthogonal. Let
where
 . Taking the transpose of the first equation and right multiplying by
. Taking the transpose of the first equation and right multiplying by  , and left multiplying the second
equation by
, and left multiplying the second
equation by  , we obtain
, we obtain
Taking the difference of the above two equations, we get
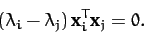 |
(484) |
Since, by hypothesis,
 , it follows
that
, it follows
that
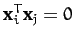 . In vector notation, this is the same
as
. In vector notation, this is the same
as
 . Hence, the eigenvectors
. Hence, the eigenvectors 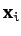 and
and
 are mutually orthogonal.
are mutually orthogonal.
Suppose that
 . In this case, we cannot conclude
that
. In this case, we cannot conclude
that
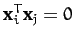 by the above argument. However, it is easily seen that any
linear combination of
by the above argument. However, it is easily seen that any
linear combination of 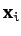 and
and  is an eigenvector
of
is an eigenvector
of 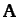 with eigenvalue
with eigenvalue 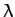 . Hence, it is possible
to define two new eigenvectors of
. Hence, it is possible
to define two new eigenvectors of 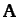 , with the eigenvalue
, with the eigenvalue
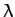 , which are mutually orthogonal. For instance,
, which are mutually orthogonal. For instance,
It should be clear that this argument can be generalized to deal with any
number of eigenvalues which take the same value.
In conclusion, a real symmetric  -dimensional matrix
possesses
-dimensional matrix
possesses  real eigenvalues, with
real eigenvalues, with  associated real eigenvectors,
which are, or can be chosen to be, mutually orthogonal.
associated real eigenvectors,
which are, or can be chosen to be, mutually orthogonal.



Next: Principal Axes of Rotation
Up: Rigid Body Rotation
Previous: Rotational Kinetic Energy
Richard Fitzpatrick
2011-03-31
![]() eigenvalues and eigenvectors of the real symmetric matrix
eigenvalues and eigenvectors of the real symmetric matrix
![]() are all real. We have
are all real. We have
![]() . In this case, we cannot conclude
that
. In this case, we cannot conclude
that
![]() by the above argument. However, it is easily seen that any
linear combination of
by the above argument. However, it is easily seen that any
linear combination of ![]() and
and ![]() is an eigenvector
of
is an eigenvector
of ![]() with eigenvalue
with eigenvalue ![]() . Hence, it is possible
to define two new eigenvectors of
. Hence, it is possible
to define two new eigenvectors of ![]() , with the eigenvalue
, with the eigenvalue
![]() , which are mutually orthogonal. For instance,
, which are mutually orthogonal. For instance,
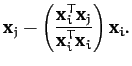
![]() -dimensional matrix
possesses
-dimensional matrix
possesses ![]() real eigenvalues, with
real eigenvalues, with ![]() associated real eigenvectors,
which are, or can be chosen to be, mutually orthogonal.
associated real eigenvectors,
which are, or can be chosen to be, mutually orthogonal.