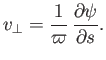Next: Axisymmetric Velocity Fields
Up: Axisymmetric Incompressible Inviscid Flow
Previous: Axisymmetric Flow
Stokes Stream Function
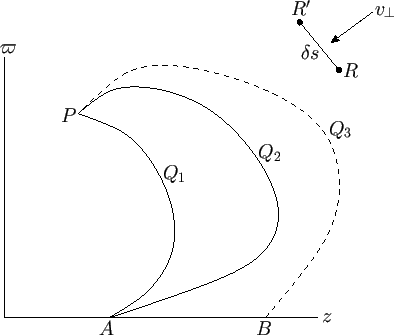
Consider a fixed point  lying on the symmetry axis, and an arbitrary point
lying on the symmetry axis, and an arbitrary point  . Let us join
. Let us join  to
to  via
two different curves,
via
two different curves,  and
and 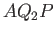 , that both lie in the same plane. (See Figure 7.1.) We shall refer to this plane as the meridian
plane. The position of a given point in the meridian plane can be specified either in terms of the cylindrical coordinates (
, that both lie in the same plane. (See Figure 7.1.) We shall refer to this plane as the meridian
plane. The position of a given point in the meridian plane can be specified either in terms of the cylindrical coordinates (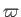 ,
,  ),
or the spherical coordinates (
),
or the spherical coordinates ( ,
,  ). If
the meridian curves
). If
the meridian curves 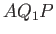 and
and 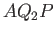 rotate about the symmetry axis then closed surfaces are formed.
Assuming that the flow pattern is incompressible, the flux of fluid from right to left (in Figure 7.1) across the surface
generated by
rotate about the symmetry axis then closed surfaces are formed.
Assuming that the flow pattern is incompressible, the flux of fluid from right to left (in Figure 7.1) across the surface
generated by 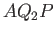 must match that in the same direction across the surface
generated by
must match that in the same direction across the surface
generated by 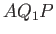 . Let us denote the flux across either of these surfaces by
. Let us denote the flux across either of these surfaces by
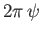 . Here,
. Here,
 is known as the Stokes stream function. If we keep
is known as the Stokes stream function. If we keep 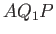 fixed, and replace
fixed, and replace 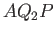 by any
other meridian curve joining
by any
other meridian curve joining  to
to 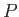 , then the value of
, then the value of  is clearly unaltered. Thus, the stream function
is clearly unaltered. Thus, the stream function  depends on the position of the arbitrary point
depends on the position of the arbitrary point 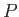 , and, possibly, on that of the fixed point
, and, possibly, on that of the fixed point  . In fact, if we
take another fixed point
. In fact, if we
take another fixed point 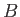 on the symmetry axis, and draw the meridian curve
on the symmetry axis, and draw the meridian curve 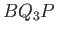 , then the flux across the
surface generated by
, then the flux across the
surface generated by 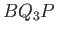 will be the same as that across the surface generated by
will be the same as that across the surface generated by 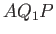 , because, by symmetry, there is no
flow across
, because, by symmetry, there is no
flow across 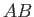 . (See Figure 7.1.) It follows that the value of
. (See Figure 7.1.) It follows that the value of  does not depend on the particular
fixed point that is used in its definition, as long as this point lies on the symmetry axis. Hence, we conclude
that the value of the stream function at
does not depend on the particular
fixed point that is used in its definition, as long as this point lies on the symmetry axis. Hence, we conclude
that the value of the stream function at 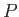 depends solely on the position of
depends solely on the position of 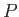 . Furthermore, if
. Furthermore, if 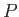 lies
on the axis then
lies
on the axis then 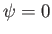 .
.
Figure 7.1:
Definition of the Stokes stream function.
 |
Consider two neighboring points, 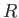 and
and  , lying in the meridian plane. (See Figure 7.1.) The flux from right to left across the surface
generated by revolving any line joining
, lying in the meridian plane. (See Figure 7.1.) The flux from right to left across the surface
generated by revolving any line joining 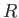 to
to  about the symmetry axis is
about the symmetry axis is
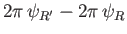 .
If the distance
.
If the distance 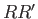 takes the infinitesimal value
takes the infinitesimal value 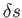 then we can write
then we can write
 |
(7.1) |
where 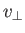 is the normal flow velocity (from right to left) across the straight-line
is the normal flow velocity (from right to left) across the straight-line 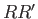 in the meridian plane. (See Figure 7.1.)
It follows that
in the meridian plane. (See Figure 7.1.)
It follows that
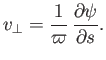 |
(7.2) |
In particular, if we suppose that 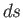 is, in turn, equal to
is, in turn, equal to 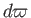 ,
, 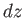 ,
, 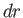 , and
, and
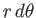 then we obtain the
following expressions for the in-plane velocity components in cylindrical and spherical coordinates:
then we obtain the
following expressions for the in-plane velocity components in cylindrical and spherical coordinates:



Next: Axisymmetric Velocity Fields
Up: Axisymmetric Incompressible Inviscid Flow
Previous: Axisymmetric Flow
Richard Fitzpatrick
2016-03-31

![]() and
and ![]() , lying in the meridian plane. (See Figure 7.1.) The flux from right to left across the surface
generated by revolving any line joining
, lying in the meridian plane. (See Figure 7.1.) The flux from right to left across the surface
generated by revolving any line joining ![]() to
to ![]() about the symmetry axis is
about the symmetry axis is
![]() .
If the distance
.
If the distance ![]() takes the infinitesimal value
takes the infinitesimal value ![]() then we can write
then we can write