


Next: Two-Dimensional Potential Flow
Up: Two-Dimensional Incompressible Inviscid Flow
Previous: Two-Dimensional Jets
- For the case of the two-dimensional motion of an incompressible fluid, determine the condition that the velocity components
satisfy the equation of continuity. Show that the magnitude of the vorticity is 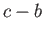 .
.
- For the case of the two-dimensional motion of an incompressible fluid, show that
are the velocity components of a possible flow pattern. Determine the stream function and sketch the streamlines.
Prove that the motion is irrotational, and find the velocity potential.
- A cylindrical vortex in an incompressible fluid is co-axial with the
 -axis, and such that
-axis, and such that 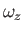 takes the constant value
takes the constant value
 for
for 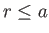 , and is zero for
, and is zero for 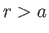 , where
, where  is a cylindrical coordinate. Show that
is a cylindrical coordinate. Show that
where 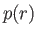 is the pressure at radius
is the pressure at radius  inside the vortex, and the circulation of the fluid outside the vortex is
inside the vortex, and the circulation of the fluid outside the vortex is
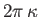 .
Deduce that
.
Deduce that
where 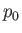 is the pressure at the center of the vortex.
is the pressure at the center of the vortex.
- Consider the cylindrical vortex discussed in Exercise 3. If
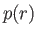 is the pressure at radius
is the pressure at radius  external to the
vortex, demonstrate that
external to the
vortex, demonstrate that
where 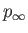 is the pressure at infinity.
is the pressure at infinity.
- Show that the stream function for the cylindrical vortex discussed in Exercises 3 and 4 is
 for
for 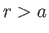 , and
, and
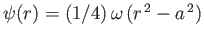 for
for 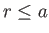 .
.
- Prove that in the two-dimensional motion of a liquid the mean tangential
fluid velocity around any small circle of radius
 is
is 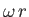 , where
, where  is the value of
is the value of
at the center of the circle. Neglect terms of order  .
.
- Show that the equation of continuity for the two-dimensional motion of an
incompressible fluid can be written
where  ,
,  are cylindrical coordinates. Demonstrate that this
equation is satisfied when
are cylindrical coordinates. Demonstrate that this
equation is satisfied when
![$ v_r=a\,k\,r^{\,n}\,\exp[-k\,(n+1)\,\theta]$](img1919.png) and
and
![$ v_\theta=a\,r^{\,n}\,\exp[-k\,(n+1)\,\theta]$](img1920.png) . Determine the stream function, and
show that the fluid speed at any point is
. Determine the stream function, and
show that the fluid speed at any point is
where  is the stream function at that point (defined such that
is the stream function at that point (defined such that 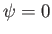 at
at  ).
).
- Demonstrate that streamlines cross at right-angles at a stagnation point in two-dimensional, incompressible,
irrotational flow.
- Consider two-dimensional, incompressible, inviscid flow. Demonstrate that the fluid motion
is governed by the following equations:
where
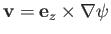 ,
,
![$ [A,B] = {\bf e}_z\cdot\nabla A \times\nabla B$](img1929.png) , and
, and
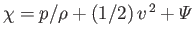 .
.
- For irrotational, incompressible, inviscid motion in two dimensions show that
where
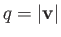 .
.



Next: Two-Dimensional Potential Flow
Up: Two-Dimensional Incompressible Inviscid Flow
Previous: Two-Dimensional Jets
Richard Fitzpatrick
2016-03-31

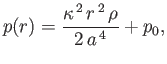
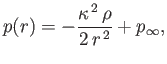
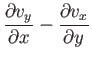

![$\displaystyle \frac{\partial\omega}{\partial t} +[\psi,\omega]$](img1923.png)