


Next: Inviscid Flow Past a
Up: Two-Dimensional Incompressible Inviscid Flow
Previous: Flow Past a Cylindrical
Motion of a Submerged Cylinder
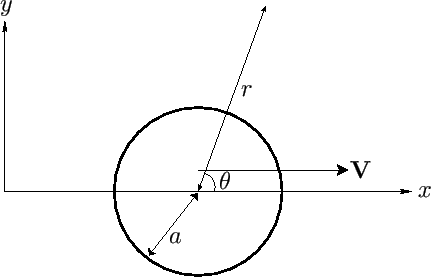
Consider the situation, illustrated in Figure 5.9, in which an impenetrable
rigid cylinder of radius  and infinite length, whose symmetry axis runs parallel to the
and infinite length, whose symmetry axis runs parallel to the  -direction, is moving
through an incompressible, inviscid fluid at the time-dependent velocity
-direction, is moving
through an incompressible, inviscid fluid at the time-dependent velocity
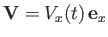 .
Assuming that the fluid and cylinder were both initially stationary, it follows that the fluid
velocity field was initially irrotational. Thus, according to the Kelvin circulation theorem, the fluid velocity field
remains irrotational when the cylinder starts to move. Thus, we can write
.
Assuming that the fluid and cylinder were both initially stationary, it follows that the fluid
velocity field was initially irrotational. Thus, according to the Kelvin circulation theorem, the fluid velocity field
remains irrotational when the cylinder starts to move. Thus, we can write
 |
(5.84) |
where 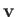 is the fluid velocity.
Moreover, because the fluid is incompressible, we have
is the fluid velocity.
Moreover, because the fluid is incompressible, we have
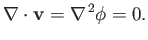 |
(5.85) |
Figure 5.9:
Cylinder moving through an inviscid fluid
 |
Let  ,
,  ,
,  be Cartesian coordinates in the initial rest frame of the fluid, and let
be Cartesian coordinates in the initial rest frame of the fluid, and let  ,
,  be
cylindrical coordinates in a frame of reference that co-moves with the cylinder, as shown in Figure 5.9.
In the following, all calculations are performed in the rest frame. We expect the fluid a long way from the
cylinder to remain stationary. In other words,
be
cylindrical coordinates in a frame of reference that co-moves with the cylinder, as shown in Figure 5.9.
In the following, all calculations are performed in the rest frame. We expect the fluid a long way from the
cylinder to remain stationary. In other words,
Moreover, because the cylinder is impenetrable, we require that
 |
(5.87) |
or
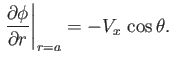 |
(5.88) |
It is easily demonstrated that the solution to Equation (5.85), subject to the boundary conditions (5.86) and (5.88),
is
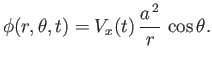 |
(5.89) |
Hence,
The general form of Bernoulli's theorem, (4.96), which applies to an irrotational flow field, yields
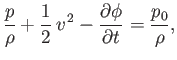 |
(5.92) |
where  is the uniform fluid mass density, and
is the uniform fluid mass density, and 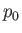 the fluid pressure at infinity. Thus, the
pressure distribution at the surface of the cylinder can be written
the fluid pressure at infinity. Thus, the
pressure distribution at the surface of the cylinder can be written
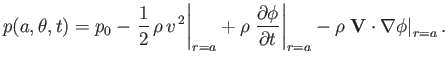 |
(5.93) |
The final term on the right-hand side of the previous equation arises because
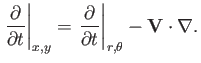 |
(5.94) |
Hence, we obtain
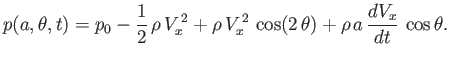 |
(5.95) |
The net force per unit length exerted on the cylinder by the fluid has the Cartesian components
It follows that
or
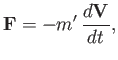 |
(5.100) |
where
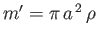 is the mass per unit length of the fluid displaced by the cylinder.
is the mass per unit length of the fluid displaced by the cylinder.
Suppose that the cylinder is subject to an external (i.e., not due to the fluid) force per unit length
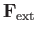 . The
equation of motion of the cylinder is thus
. The
equation of motion of the cylinder is thus
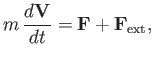 |
(5.101) |
where 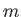 is the cylinder's mass per unit length. The previous two equations can be combined to give
is the cylinder's mass per unit length. The previous two equations can be combined to give
 |
(5.102) |
In other words, the cylinder moves under the action of the external force,
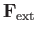 , as if its
mass per unit length were
, as if its
mass per unit length were 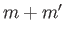 , rather than
, rather than 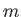 . Here,
. Here, 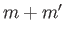 is commonly referred to as the
cylinder's virtual mass (per unit length), whereas
is commonly referred to as the
cylinder's virtual mass (per unit length), whereas 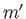 is termed the added
mass (per unit length).
is termed the added
mass (per unit length).
The origin of added mass is easily explained. According to Equations (5.90) and (5.91), the
total kinetic energy per unit length of the fluid surrounding the cylinder is
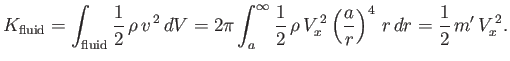 |
(5.103) |
However, the kinetic energy per unit length of the cylinder is
 |
(5.104) |
Thus, the total kinetic energy per unit length is
 |
(5.105) |
In other words, the kinetic energy of the fluid surrounding the cylinder can be accounted for by supposing that
a mass (per unit length) 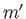 of the fluid co-moves with the cylinder, and that the remainder of the fluid remains stationary. This
entrained fluid mass accounts for the added mass of the cylinder. Note that the added mass is independent of the
speed of the cylinder (i.e., it is the same whether the cylinder moves slowly or rapidly.) In the present case, the added mass is equal to the mass of the displaced fluid. However, this is not
a general rule. (In general, the added mass of a object moving through an
inviscid fluid is proportional to the displaced mass, but the constant of
proportionality is not necessarily unity, and depends on the shape of the object.)
of the fluid co-moves with the cylinder, and that the remainder of the fluid remains stationary. This
entrained fluid mass accounts for the added mass of the cylinder. Note that the added mass is independent of the
speed of the cylinder (i.e., it is the same whether the cylinder moves slowly or rapidly.) In the present case, the added mass is equal to the mass of the displaced fluid. However, this is not
a general rule. (In general, the added mass of a object moving through an
inviscid fluid is proportional to the displaced mass, but the constant of
proportionality is not necessarily unity, and depends on the shape of the object.)
Let us generalize the previous calculation to allow the cylinder to move in any direction in the  -
- plane: that is,
plane: that is,
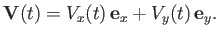 |
(5.106) |
Furthermore, let the fluid possess the initial circulation
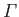 in the
in the  -
- plane. According to the
Kelvin circulation theorem, this circulation remains constant in time. Thus, we must now solve Equation (5.85)
subject to the boundary conditions
plane. According to the
Kelvin circulation theorem, this circulation remains constant in time. Thus, we must now solve Equation (5.85)
subject to the boundary conditions
and
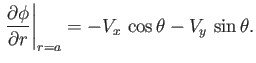 |
(5.108) |
It is easily demonstrated that the appropriate solution is
 |
(5.109) |
Hence,
Bernoulli's theorem yields
 |
(5.112) |
where we have assumed that the fluid and cylinder are both situated in a gravitational field of uniform acceleration
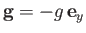 . Thus, the
pressure distribution at the surface of the cylinder can be written
. Thus, the
pressure distribution at the surface of the cylinder can be written
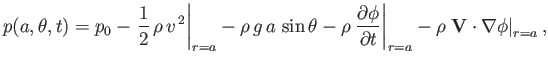 |
(5.113) |
which yields
It follows from Equations (5.96) and (5.97) that the force per unit length exerted on the
cylinder by the fluid has the Cartesian components
Here, the first terms on the right-hand sides of the previous two equations are the components of the
lift (per unit length) acting on the cylinder, due to the fluid circulation, whereas the final term on the right-hand side of the
second equation is the buoyancy force (per unit length) acting on the cylinder.
The cylinder's equation of motion,
leads to
where
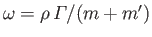 , and
, and 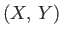 are the Cartesian components of the cylinder's axis.
Let us assume that
are the Cartesian components of the cylinder's axis.
Let us assume that
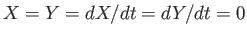 at
at  . It follows that
. It follows that
Consider, first, the case in which there is no circulation of the flow: that is,
 . In this case,
the previous two equations reduce to
. In this case,
the previous two equations reduce to
In other words, the cylinder moves vertically (i.e., in the  -direction) with the constant acceleration
-direction) with the constant acceleration
 |
(5.125) |
where 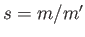 is the cylinder's specific gravity. It follows that if the cylinder is much denser than the
fluid (i.e.,
is the cylinder's specific gravity. It follows that if the cylinder is much denser than the
fluid (i.e., 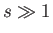 ) then it accelerates downward at the acceleration due to gravity: that is,
) then it accelerates downward at the acceleration due to gravity: that is, 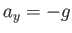 . However, if the
cylinder is much less dense than the fluid (i.e.,
. However, if the
cylinder is much less dense than the fluid (i.e., 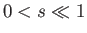 ) then it accelerates upward at the acceleration
due to gravity: that is
) then it accelerates upward at the acceleration
due to gravity: that is  . Note that, in the latter case, the upward acceleration is limited by the cylinder's
added mass (i.e., in the absence of added mass, the acceleration would be infinite.)
. Note that, in the latter case, the upward acceleration is limited by the cylinder's
added mass (i.e., in the absence of added mass, the acceleration would be infinite.)
In the general case, in which the fluid circulation is non-zero, the trajectory of the cylinder is a cycloid. In particular,
assuming that 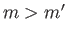 , the lift acting on the cylinder prevents it from falling through the fluid a distance greater than
, the lift acting on the cylinder prevents it from falling through the fluid a distance greater than
![$ 2\,[(m-m')/(m+m')]\,(g/\omega^{\,2})$](img1865.png) . Once the cylinder has fallen through this distance, it starts to rise again, until
it attains its original height, and the motion then repeats itself ad infinitum. Moreover, the cylinder simultaneously
moves horizontally (i.e. in the
. Once the cylinder has fallen through this distance, it starts to rise again, until
it attains its original height, and the motion then repeats itself ad infinitum. Moreover, the cylinder simultaneously
moves horizontally (i.e. in the  -direction) at the mean velocity
-direction) at the mean velocity
![$ -[(m-m')/(m+m')]\,(g/\omega)$](img1866.png) .
.



Next: Inviscid Flow Past a
Up: Two-Dimensional Incompressible Inviscid Flow
Previous: Flow Past a Cylindrical
Richard Fitzpatrick
2016-03-31
![]() ,
, ![]() ,
, ![]() be Cartesian coordinates in the initial rest frame of the fluid, and let
be Cartesian coordinates in the initial rest frame of the fluid, and let ![]() ,
, ![]() be
cylindrical coordinates in a frame of reference that co-moves with the cylinder, as shown in Figure 5.9.
In the following, all calculations are performed in the rest frame. We expect the fluid a long way from the
cylinder to remain stationary. In other words,
be
cylindrical coordinates in a frame of reference that co-moves with the cylinder, as shown in Figure 5.9.
In the following, all calculations are performed in the rest frame. We expect the fluid a long way from the
cylinder to remain stationary. In other words,
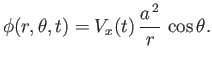
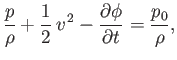
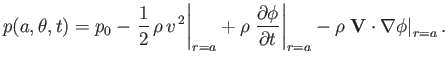
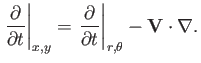
![]() . The
equation of motion of the cylinder is thus
. The
equation of motion of the cylinder is thus

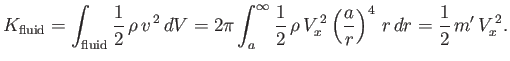


![]() -
-![]() plane: that is,
plane: that is,
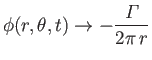
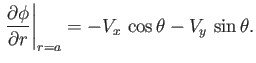


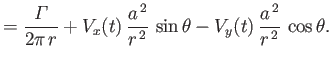

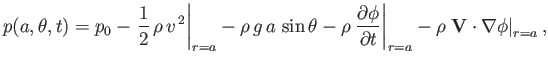
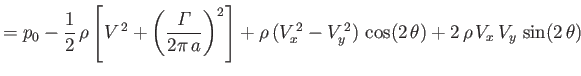
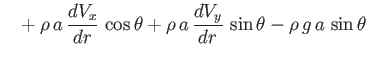
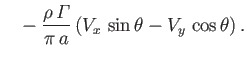
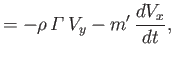
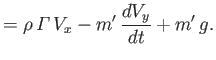
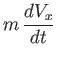

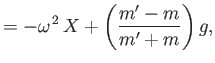
![$\displaystyle = \left(\frac{m-m'}{m+m'}\right)\,\frac{g}{\omega^{\,2}}\left[\sin(\omega\,t)-\omega\,t\right],$](img1854.png)
![$\displaystyle = -\left(\frac{m-m'}{m+m'}\right)\,\frac{g}{\omega^{\,2}}\left[1-\cos(\omega\,t)\right].$](img1856.png)
![]() . In this case,
the previous two equations reduce to
. In this case,
the previous two equations reduce to
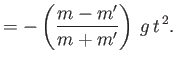

![]() , the lift acting on the cylinder prevents it from falling through the fluid a distance greater than
, the lift acting on the cylinder prevents it from falling through the fluid a distance greater than
![]() . Once the cylinder has fallen through this distance, it starts to rise again, until
it attains its original height, and the motion then repeats itself ad infinitum. Moreover, the cylinder simultaneously
moves horizontally (i.e. in the
. Once the cylinder has fallen through this distance, it starts to rise again, until
it attains its original height, and the motion then repeats itself ad infinitum. Moreover, the cylinder simultaneously
moves horizontally (i.e. in the ![]() -direction) at the mean velocity
-direction) at the mean velocity
![]() .
.