


Next: Two-Dimensional Incompressible Inviscid Flow
Up: Incompressible Inviscid Flow
Previous: Irrotational Flow
- Liquid is led steadily through a pipeline that passes over a hill of height
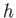 into the valley below, the
speed at the crest being
into the valley below, the
speed at the crest being 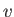 . Show that, by properly adjusting the ratio of the cross-sectional areas of the pipe
at the crest and in the valley, the pressure may be equalized at these two places. (Milne-Thomson 1958.)
. Show that, by properly adjusting the ratio of the cross-sectional areas of the pipe
at the crest and in the valley, the pressure may be equalized at these two places. (Milne-Thomson 1958.)
- Water of mass density
 and pressure
and pressure  flows through a curved pipe of
uniform cross-sectional area
flows through a curved pipe of
uniform cross-sectional area  , whose radius of curvature is
, whose radius of curvature is 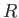 , at the
uniform speed
, at the
uniform speed 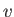 . Demonstrate that there is a net force per unit length
. Demonstrate that there is a net force per unit length
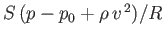 acting on the
pipe, and that this force is everywhere directed away from the pipe's local center of curvature. Here,
acting on the
pipe, and that this force is everywhere directed away from the pipe's local center of curvature. Here, 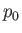 is atmospheric pressure.
is atmospheric pressure.
- Water is held in a right circular conical tank whose apex lies vertically below the center of its
base. The water initially fills the tank to a height
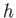 above the vertex. Let
above the vertex. Let  be the initial
radius of the surface of the water inside the tank. A small hole of area
be the initial
radius of the surface of the water inside the tank. A small hole of area  (that is much less than
(that is much less than
 )
is made at the bottom of the tank. Demonstrate that the time required to empty the tank is at least
)
is made at the bottom of the tank. Demonstrate that the time required to empty the tank is at least
- Water is held in a spherical tank of radius
 , and initially fills the tank to a height
, and initially fills the tank to a height 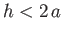 above
its lowest point. A small hole of area
above
its lowest point. A small hole of area  (that is much less than
(that is much less than
 ) is made
at the bottom of the tank. Demonstrate that the time required to empty the tank is at least
) is made
at the bottom of the tank. Demonstrate that the time required to empty the tank is at least
- Water is held in two contiguous tanks whose cross-sectional areas,
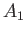 and
and 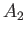 , are independent of height. A
small hole of area
, are independent of height. A
small hole of area  (where
(where 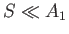 ,
, 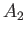 ) is made in the wall connecting the tanks. Assuming that the initial
difference in water level between the two tanks is
) is made in the wall connecting the tanks. Assuming that the initial
difference in water level between the two tanks is 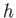 , show that the time
required for the water levels to equilibrate is at least
, show that the time
required for the water levels to equilibrate is at least
- For a channel of width
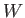 , having a discharge rate
, having a discharge rate  , show that there is
a critical depth
, show that there is
a critical depth 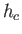 , where
, where
which must be exceeded before a hydraulic jump is possible.
- Show that for a stationary hydraulic jump in a rectangular channel, the
upstream Froude number
 , and the downstream Froude number
, and the downstream Froude number
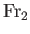 ,
are related by
,
are related by
- Consider a simply-connected volume
 whose boundary is the surface
whose boundary is the surface  . Suppose that
. Suppose that  contains an
incompressible fluid whose motion is irrotational. Let the velocity potential
contains an
incompressible fluid whose motion is irrotational. Let the velocity potential 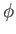 be constant over
be constant over
 . Prove that
. Prove that 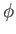 has the same constant value throughout
has the same constant value throughout  . [Hint: Consider the identity
. [Hint: Consider the identity
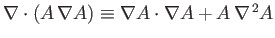 .]
.]
- In Exercise 8, suppose that, instead of
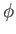 taking a constant value on the boundary, the
normal velocity is everywhere zero on the boundary. Show that
taking a constant value on the boundary, the
normal velocity is everywhere zero on the boundary. Show that 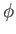 is constant throughout
is constant throughout  .
.
- An incompressible fluid flows in a simply-connected volume
 bounded by a surface
bounded by a surface  .
The normal flow at the boundary is prescribed. Show that the flow pattern with the lowest kinetic
energy is irrotational. This result is known as the Kelvin minimum energy theorem. [Hint: Try writing
.
The normal flow at the boundary is prescribed. Show that the flow pattern with the lowest kinetic
energy is irrotational. This result is known as the Kelvin minimum energy theorem. [Hint: Try writing
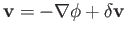 , where
, where 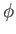 is the
velocity potential of the irrotational flow pattern. Let
is the
velocity potential of the irrotational flow pattern. Let
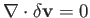 throughout
throughout  , and
, and
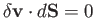 on
on  . Show that the kinetic energy is lowest when
. Show that the kinetic energy is lowest when
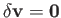 throughout
throughout  .]
.]



Next: Two-Dimensional Incompressible Inviscid Flow
Up: Incompressible Inviscid Flow
Previous: Irrotational Flow
Richard Fitzpatrick
2016-03-31
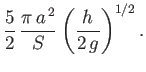
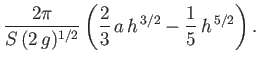
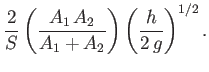
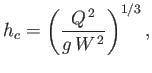
![$\displaystyle {\rm Fr}_2^{\,2} =\frac{8\,{\rm Fr}_1^{\,2}}{[(1+8\,{\rm Fr}_1^{\,2})^{1/2}-1]^{\,3}}.
$](img1608.png)
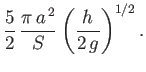
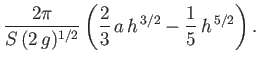
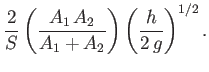
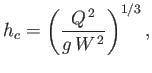
![$\displaystyle {\rm Fr}_2^{\,2} =\frac{8\,{\rm Fr}_1^{\,2}}{[(1+8\,{\rm Fr}_1^{\,2})^{1/2}-1]^{\,3}}.
$](img1608.png)