


Next: Vortex Lines, Vortex Tubes,
Up: Incompressible Inviscid Flow
Previous: Tidal Bores
Figure 4.8:
Flow over a broad-crested weir.
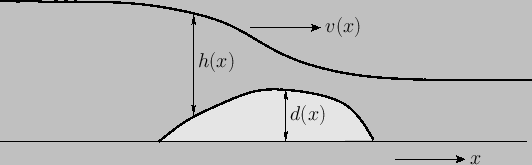 |
Consider the situation, illustrated in Figure 4.8, in which a broad-crested weir is placed in a shallow stream.
The purpose of the weir is to impede the flow in such a manner that there is a transition from sub-critical flow, upstream of the weir, to super-critical flow, immediately downstream of the weir. (There is usually a transition back to sub-critical flow, via a hydraulic jump, some way downstream of the weir.)
Let  measure horizontal distance, and let
measure horizontal distance, and let  ,
, 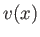 , and
, and 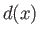 be the stream depth, stream
velocity, and the height of the weir above the stream bed, respectively. (Here, we are assuming that the velocity
remains uniform across the stream at any point on the weir.) A direct generalization of the analysis of Section 4.7
reveals that
be the stream depth, stream
velocity, and the height of the weir above the stream bed, respectively. (Here, we are assuming that the velocity
remains uniform across the stream at any point on the weir.) A direct generalization of the analysis of Section 4.7
reveals that
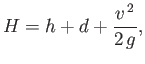 |
(4.64) |
and
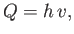 |
(4.65) |
where (via continuity) the flow rate,  , is not a function of
, is not a function of  . It follows that
. It follows that
 |
(4.66) |
where  is defined in Equation (4.21).
Suppose that the weir attains its maximum height,
is defined in Equation (4.21).
Suppose that the weir attains its maximum height, 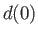 , at
, at  . It follows that
. It follows that  passes through a
minimum value at
passes through a
minimum value at  . Hence, we would expect
. Hence, we would expect  to also pass through its minimum value at
to also pass through its minimum value at  . It follows
that
. It follows
that
where use has been made of Equations (4.22) and (4.23).
However,
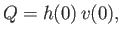 |
(4.69) |
where 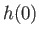 is the depth of the stream as its passes over the highest point of the weir. Thus, we deduce that
is the depth of the stream as its passes over the highest point of the weir. Thus, we deduce that
![$\displaystyle Q = [g\,h^{\,3}(0)]^{1/2} = \left(\frac{2}{3}\right)^{3/2}\left(g\left[H-d(0)\right]^{\,3}\right)^{1/2}.$](img1534.png) |
(4.70) |
In other words, the flow rate (per unit width) is very simply related to the depth of the stream as it passes over the highest
point of the weir, or, alternatively, the depth of the highest point of the weir below the water surface in the reservoir feeding
the stream. For this reason, weirs are commonly used as devices to both measure and control flow rates in streams.



Next: Vortex Lines, Vortex Tubes,
Up: Incompressible Inviscid Flow
Previous: Tidal Bores
Richard Fitzpatrick
2016-03-31

![]() measure horizontal distance, and let
measure horizontal distance, and let ![]() ,
, ![]() , and
, and ![]() be the stream depth, stream
velocity, and the height of the weir above the stream bed, respectively. (Here, we are assuming that the velocity
remains uniform across the stream at any point on the weir.) A direct generalization of the analysis of Section 4.7
reveals that
be the stream depth, stream
velocity, and the height of the weir above the stream bed, respectively. (Here, we are assuming that the velocity
remains uniform across the stream at any point on the weir.) A direct generalization of the analysis of Section 4.7
reveals that
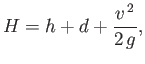
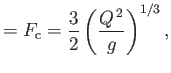
![$\displaystyle Q = [g\,h^{\,3}(0)]^{1/2} = \left(\frac{2}{3}\right)^{3/2}\left(g\left[H-d(0)\right]^{\,3}\right)^{1/2}.$](img1534.png)