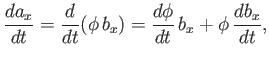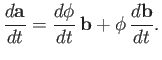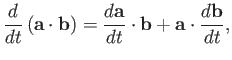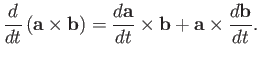Next: Line Integrals
Up: Vectors and Vector Fields
Previous: Vector Triple Product
Vector Calculus
Suppose that vector 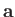 varies with time, so that
varies with time, so that
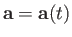 . The time
derivative of the vector is defined
. The time
derivative of the vector is defined
![$\displaystyle \frac{d {\bf a}}{dt} = \lim_{\delta t\rightarrow 0} \left[\frac{{\bf a}(t+\delta t) - {\bf a}(t)} {\delta t}\right].$](img6433.png) |
(A.63) |
When written out in component form this becomes
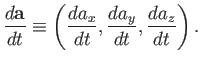 |
(A.64) |
Suppose that 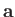 is, in fact, the product of a scalar
is, in fact, the product of a scalar 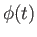 and another vector
and another vector
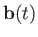 . What now is the time derivative of
. What now is the time derivative of 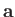 ? We have
? We have
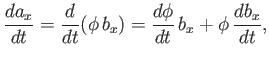 |
(A.65) |
which implies that
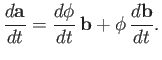 |
(A.66) |
Moreover, it is easily demonstrated that
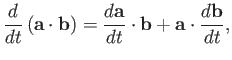 |
(A.67) |
and
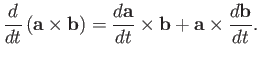 |
(A.68) |
Hence, it can be seen that the laws of vector differentiation are analogous to those in
conventional calculus.



Next: Line Integrals
Up: Vectors and Vector Fields
Previous: Vector Triple Product
Richard Fitzpatrick
2016-03-31
![$\displaystyle \frac{d {\bf a}}{dt} = \lim_{\delta t\rightarrow 0} \left[\frac{{\bf a}(t+\delta t) - {\bf a}(t)} {\delta t}\right].$](img6433.png)
![$\displaystyle \frac{d {\bf a}}{dt} = \lim_{\delta t\rightarrow 0} \left[\frac{{\bf a}(t+\delta t) - {\bf a}(t)} {\delta t}\right].$](img6433.png)
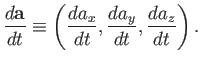
![]() is, in fact, the product of a scalar
is, in fact, the product of a scalar ![]() and another vector
and another vector
![]() . What now is the time derivative of
. What now is the time derivative of ![]() ? We have
? We have