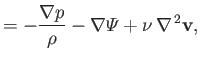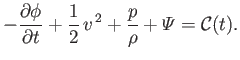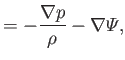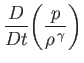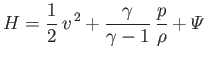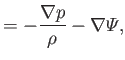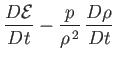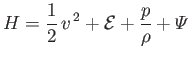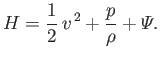- Equations (1.66), (1.75), and (1.87) can be combined to give the following energy conservation equation
for a non-ideal compressible fluid:
where 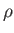 is the mass density,
is the mass density, 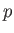 the pressure,
the pressure, 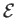 the internal energy per unit mass,
the internal energy per unit mass, 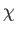 the
viscous energy dissipation rate per unit volume, and
the
viscous energy dissipation rate per unit volume, and 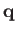 the heat flux density. We also have
the heat flux density. We also have
where 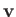 is the fluid velocity,
is the fluid velocity, 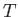 the temperature, and
the temperature, and 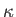 the thermal conductivity. According to a standard theorem in thermodynamics (Reif 1965),
the thermal conductivity. According to a standard theorem in thermodynamics (Reif 1965),
where 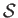 is the entropy per unit mass. Moreover, the entropy flux density at a given point
in the fluid is (Hazeltine and Waelbroeck 2004)
is the entropy per unit mass. Moreover, the entropy flux density at a given point
in the fluid is (Hazeltine and Waelbroeck 2004)
where the first term on the right-hand side is due to direct entropy convection by the fluid, and the second is the entropy
flux density associated with heat conduction.
Derive an entropy conservation equation of the form
where 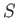 is the net amount of entropy contained in some fixed volume
is the net amount of entropy contained in some fixed volume 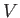 ,
,
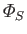 the entropy flux out of
the entropy flux out of 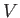 , and
, and
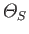 the
net rate of entropy creation within
the
net rate of entropy creation within 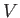 . Give expressions for
. Give expressions for 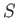 ,
,
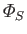 , and
, and
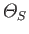 . Demonstrate that
the entropy creation rate per unit volume is
. Demonstrate that
the entropy creation rate per unit volume is
Finally, show that
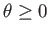 , in accordance with the second law of thermodynamics.
, in accordance with the second law of thermodynamics.
- The Navier-Stokes equation for an incompressible fluid of uniform mass density
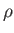 takes the form
takes the form
where 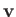 is the fluid velocity,
is the fluid velocity, 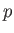 the pressure,
the pressure,
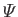 the potential energy per unit mass, and
the potential energy per unit mass, and 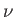 the (uniform) kinematic viscosity. The incompressibility constraint requires that
the (uniform) kinematic viscosity. The incompressibility constraint requires that
Finally, the quantity
is generally referred to as the fluid vorticity.
Derive the following vorticity evolution equation from
the Navier-Stokes equation:
- Consider two-dimensional incompressible fluid flow. Let the velocity field take the form
Demonstrate that the equations of incompressible fluid flow (see Exercise 2) can be satisfied by writing
where
and
Here,
![$ [A,\,B]\equiv {\bf e}_z\cdot\nabla A\times \nabla B$](img540.png) , and
, and
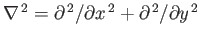 . Furthermore, the quantity
. Furthermore, the quantity 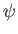 is termed a stream function,
because
is termed a stream function,
because
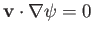 . In other words, the fluid flow is everywhere parallel to contours of
. In other words, the fluid flow is everywhere parallel to contours of 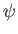 .
.
- Consider incompressible irrotational flow: that is, flow that satisfies
as well as
Here, 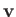 is the fluid velocity,
is the fluid velocity, 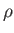 the uniform mass density,
the uniform mass density, 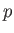 the pressure,
the pressure,
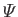 the potential energy
per unit mass, and
the potential energy
per unit mass, and 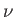 the (uniform) kinematic viscosity.
the (uniform) kinematic viscosity.
Demonstrate that the previous equations can
be satisfied by writing
where
and
Here,
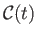 is a spatial constant. This type of flow is known as potential flow, because the velocity
field is derived from a scalar potential.
is a spatial constant. This type of flow is known as potential flow, because the velocity
field is derived from a scalar potential.
- The equations of inviscid adiabatic ideal gas flow are
Here, 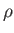 is the mass density,
is the mass density, 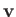 the flow velocity,
the flow velocity, 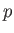 the pressure,
the pressure,
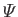 the
potential energy per unit mass, and
the
potential energy per unit mass, and 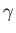 the (uniform) ratio of specific heats.
Suppose that the pressure and potential energy are both time independent: that is,
the (uniform) ratio of specific heats.
Suppose that the pressure and potential energy are both time independent: that is,
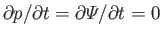 .
.
Demonstrate that
is a constant of the motion. In other words, 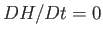 . This result is known as Bernoulli's theorem.
. This result is known as Bernoulli's theorem.
- The equations of inviscid adiabatic non-ideal gas flow are
Here, 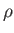 is the mass density,
is the mass density, 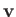 the flow velocity,
the flow velocity, 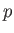 the pressure,
the pressure,
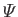 the
potential energy per unit mass, and
the
potential energy per unit mass, and 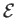 the internal energy per unit mass.
Suppose that the pressure and potential energy are both time independent: that is,
the internal energy per unit mass.
Suppose that the pressure and potential energy are both time independent: that is,
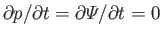 .
Demonstrate that
.
Demonstrate that
is a constant of the motion. In other words, 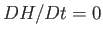 . This result is a more general form of Bernoulli's theorem.
. This result is a more general form of Bernoulli's theorem.
- Demonstrate that Bernoulli's theorem for incompressible, inviscid fluid flow takes the form
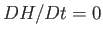 , where
, where
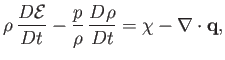
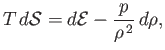
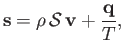
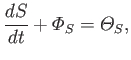
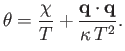
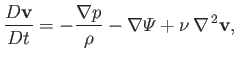
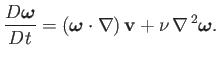
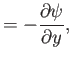
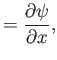
![$\displaystyle \frac{\partial\omega}{\partial t}+[\psi,\,\omega] = \nu\,\nabla^{\,2}\omega,
$](img538.png)