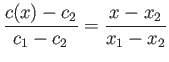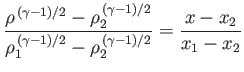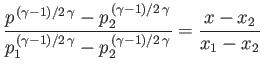Next: Exercises
Up: One-Dimensional Compressible Inviscid Flow
Previous: Piston-Generated Shock Wave
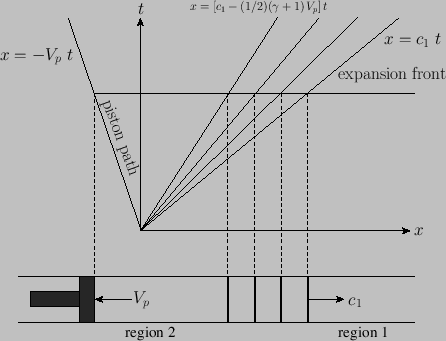
Consider the situation illustrated in Figure 14.3 in which, at  , a tight-fitting piston is suddenly withdrawn from a stationary gas, contained in a uniform tube, at the
steady speed
, a tight-fitting piston is suddenly withdrawn from a stationary gas, contained in a uniform tube, at the
steady speed 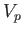 , generating an expansion wave that propagates away from the piston, and into the gas. Suppose that the
piston is located at
, generating an expansion wave that propagates away from the piston, and into the gas. Suppose that the
piston is located at  at
at  , and moves in the
, and moves in the 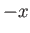 -direction.
As described in Section 14.4, the expansion wave is isentropic.
-direction.
As described in Section 14.4, the expansion wave is isentropic.
Figure 14.3:
A piston-generated expansion wave.
 |
The sudden withdrawal of the piston creates a step-function change in the flow speed, pressure, density, and temperature, of the gas inside the tube, such that the immediately adjacent gas moves with the
piston. As described in Section 14.4, this step function flattens as the expansion wave begins to propagate. Locally, within the wave, the disturbance travels at the
sound speed. Because the temperature varies across the wave (which starts out as a step in this variable), the local speed of disturbance propagation
also varies across the wave. On the edge of the wave adjacent to the region of undisturbed gas, which we shall denote region 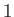 , the temperature and propagation speed are greatest.
On the opposite edge, the temperature and propagation speed are least. Let the region lying between the piston and the left edge of the expansion wave be denoted region
, the temperature and propagation speed are greatest.
On the opposite edge, the temperature and propagation speed are least. Let the region lying between the piston and the left edge of the expansion wave be denoted region 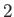 .
In region
.
In region 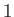 , the flow speed, pressure, density, and temperature, of the gas are
, the flow speed, pressure, density, and temperature, of the gas are 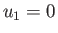 ,
, 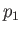 ,
, 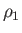 , and
, and 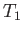 , respectively. On the
other hand, in region
, respectively. On the
other hand, in region 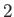 , the flow speed, pressure, density, and temperature, of the gas are
, the flow speed, pressure, density, and temperature, of the gas are 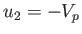 (i.e., the gas in region 2 is co-moving with the
piston),
(i.e., the gas in region 2 is co-moving with the
piston),  ,
, 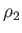 , and
, and  , respectively.
As shown in Figure 14.3, the expansion wave expands, or ``fans'' out, as it propagates. In fact, the
, respectively.
As shown in Figure 14.3, the expansion wave expands, or ``fans'' out, as it propagates. In fact, the  -
-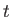 plot is a fan of constant sonic speed lines
that show the development of the wave. These lines are called characteristics, and follow the path of local isentropic disturbances.
The absolute speed of the disturbance is the sum of the local sonic speed and the local gas flow speed. The
terminating characteristic on the right has slope
plot is a fan of constant sonic speed lines
that show the development of the wave. These lines are called characteristics, and follow the path of local isentropic disturbances.
The absolute speed of the disturbance is the sum of the local sonic speed and the local gas flow speed. The
terminating characteristic on the right has slope 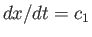 , where
, where  is the region-
is the region-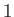 sound speed. The terminating characteristic on the left
has the slope
sound speed. The terminating characteristic on the left
has the slope
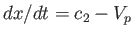 , where
, where 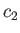 is the region-
is the region-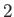 sound speed. The latter slope may be either positive or negative, depending on whether
sound speed. The latter slope may be either positive or negative, depending on whether
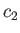 is greater than, or less than,
is greater than, or less than, 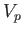 .
.
Making use of isentropic relationships (see Section 14.3), we can explicitly evaluate the structure of the fan as follows. In terms of  , the local sonic speed in the fan can be written
[cf., Equation (14.47)]
, the local sonic speed in the fan can be written
[cf., Equation (14.47)]
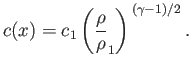 |
(14.136) |
Moreover, the relationship between the gas speed, 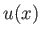 , and the density in the wave is [cf., Equation (14.48)]
, and the density in the wave is [cf., Equation (14.48)]
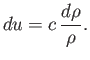 |
(14.137) |
The previous two expressions yield [cf., Equation (14.50)]
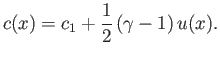 |
(14.138) |
Hence, the absolute disturbance speed in the fan is [cf., Equation (14.51)]
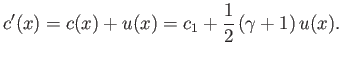 |
(14.139) |
In particular, the terminating characteristic on the left (for which 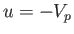 ) has the slope
) has the slope
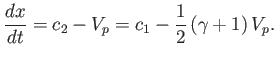 |
(14.140) |
It follows that
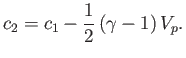 |
(14.141) |
Standard isentropic relations (see Section 14.3) then yield the density and pressure changes across the fan:
Here, use has been made of the fact that
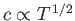 . At the critical piston withdrawal speed
. At the critical piston withdrawal speed
![$ V_p= [2/(\gamma-1)]\,c_1$](img5564.png) , the
pressure and density in region
, the
pressure and density in region 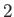 are both reduced to zero, and the terminating characteristic on the left co-moves with the
piston. Any further increase in the withdrawal speed makes no difference to the flow.
are both reduced to zero, and the terminating characteristic on the left co-moves with the
piston. Any further increase in the withdrawal speed makes no difference to the flow.
The equation of motion of the right edge of the expansion wave is
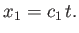 |
(14.144) |
Likewise, the equation of motion of the left edge is
![$\displaystyle x_2=\left[c_1-\frac{1}{2}\,(\gamma+1)\,V_p\right]t.$](img5566.png) |
(14.145) |
Finally, the equation of motion of a general point in the expansion wave is
![$\displaystyle x =\left[c_1+\frac{1}{2}\,(\gamma+1)\,u\right]t.$](img5567.png) |
(14.146) |
The previous three equations can be combined to give
![$\displaystyle u(x) = \left[-1+\left(\frac{x-x_2}{x_1-x_2}\right)\right]V_p$](img5568.png) |
(14.147) |
for
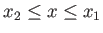 . In other words, the flow speed varies linearly with
. In other words, the flow speed varies linearly with  inside the expansion wave.
It follows from Equations (14.138) and (14.141) that
inside the expansion wave.
It follows from Equations (14.138) and (14.141) that
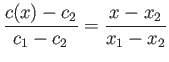 |
(14.148) |
for
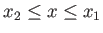 . Thus, the sound speed also varies linearly with
. Thus, the sound speed also varies linearly with  inside the expansion wave.
However, according to Equation (14.136),
inside the expansion wave.
However, according to Equation (14.136),
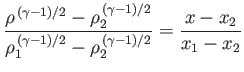 |
(14.149) |
for
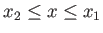 .
Furthermore, standard isentropic relations yield
.
Furthermore, standard isentropic relations yield
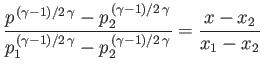 |
(14.150) |
for
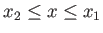 . Thus, neither the density nor the pressure vary linearly with
. Thus, neither the density nor the pressure vary linearly with  inside the expansion wave.
inside the expansion wave.



Next: Exercises
Up: One-Dimensional Compressible Inviscid Flow
Previous: Piston-Generated Shock Wave
Richard Fitzpatrick
2016-03-31

![]() , the temperature and propagation speed are greatest.
On the opposite edge, the temperature and propagation speed are least. Let the region lying between the piston and the left edge of the expansion wave be denoted region
, the temperature and propagation speed are greatest.
On the opposite edge, the temperature and propagation speed are least. Let the region lying between the piston and the left edge of the expansion wave be denoted region ![]() .
In region
.
In region ![]() , the flow speed, pressure, density, and temperature, of the gas are
, the flow speed, pressure, density, and temperature, of the gas are ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , respectively. On the
other hand, in region
, respectively. On the
other hand, in region ![]() , the flow speed, pressure, density, and temperature, of the gas are
, the flow speed, pressure, density, and temperature, of the gas are ![]() (i.e., the gas in region 2 is co-moving with the
piston),
(i.e., the gas in region 2 is co-moving with the
piston), ![]() ,
, ![]() , and
, and ![]() , respectively.
As shown in Figure 14.3, the expansion wave expands, or ``fans'' out, as it propagates. In fact, the
, respectively.
As shown in Figure 14.3, the expansion wave expands, or ``fans'' out, as it propagates. In fact, the ![]() -
-![]() plot is a fan of constant sonic speed lines
that show the development of the wave. These lines are called characteristics, and follow the path of local isentropic disturbances.
The absolute speed of the disturbance is the sum of the local sonic speed and the local gas flow speed. The
terminating characteristic on the right has slope
plot is a fan of constant sonic speed lines
that show the development of the wave. These lines are called characteristics, and follow the path of local isentropic disturbances.
The absolute speed of the disturbance is the sum of the local sonic speed and the local gas flow speed. The
terminating characteristic on the right has slope ![]() , where
, where ![]() is the region-
is the region-![]() sound speed. The terminating characteristic on the left
has the slope
sound speed. The terminating characteristic on the left
has the slope
![]() , where
, where ![]() is the region-
is the region-![]() sound speed. The latter slope may be either positive or negative, depending on whether
sound speed. The latter slope may be either positive or negative, depending on whether
![]() is greater than, or less than,
is greater than, or less than, ![]() .
.
![]() , the local sonic speed in the fan can be written
[cf., Equation (14.47)]
, the local sonic speed in the fan can be written
[cf., Equation (14.47)]
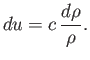
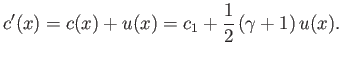
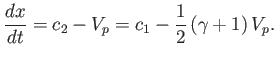
![$\displaystyle = \left[1-\frac{1}{2}\,(\gamma-1)\,\frac{V_p}{c_1}\right]^{\,2/(\gamma-1)},$](img5561.png)
![$\displaystyle = \left[1-\frac{1}{2}\,(\gamma-1)\,\frac{V_p}{c_1}\right]^{\,2\,\gamma/(\gamma-1)}.$](img5562.png)
![$\displaystyle x_2=\left[c_1-\frac{1}{2}\,(\gamma+1)\,V_p\right]t.$](img5566.png)
![$\displaystyle x =\left[c_1+\frac{1}{2}\,(\gamma+1)\,u\right]t.$](img5567.png)
![$\displaystyle u(x) = \left[-1+\left(\frac{x-x_2}{x_1-x_2}\right)\right]V_p$](img5568.png)