Next: Another Useful Lemma
Up: Terrestrial Ocean Tides
Previous: Useful Lemma
Let 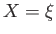 ,
, 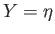 ,
,
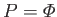 , and
, and
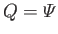 in Equations (12.191)-(12.196). It
follows that [cf., Equation (12.161)]
in Equations (12.191)-(12.196). It
follows that [cf., Equation (12.161)]
where
Here, use has been made of Equations (12.186) and (12.190). Furthermore [cf., Equations (12.159) and (12.160)],
Let
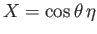 ,
,
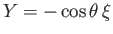 ,
,
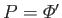 , and
, and
 in Equations (12.191)-(12.196). It
follows that
in Equations (12.191)-(12.196). It
follows that
where
Furthermore,
Substitution of Equations (12.211), (12.212), (12.217), and (12.218) into Equations (12.187) and (12.188) yields
where
Equations (12.219) and (12.220) can be combined to give
Moreover, it follows from Equations (12.188), (12.190), (12.209), (12.210), (12.215), and (12.216) that
We have already seen that the solution of Equation (12.205), subject to the boundary condition (12.204), is
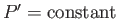 . It follows
that the solution of Equation (12.223), subject to the boundary condition (12.225), is
. It follows
that the solution of Equation (12.223), subject to the boundary condition (12.225), is
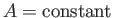 .
Analogous arguments reveal that the solution of Equation (12.224), subject to the boundary condition (12.226), is
.
Analogous arguments reveal that the solution of Equation (12.224), subject to the boundary condition (12.226), is 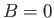 . Hence,
we deduce that the Laplace tidal equations, (12.186)-(12.188), are equivalent to the following set of equations:
. Hence,
we deduce that the Laplace tidal equations, (12.186)-(12.188), are equivalent to the following set of equations:
where
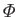 ,
,
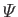 ,
,
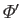 ,
,
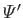 , and
, and 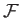 are defined in Equations (12.211), (12.212), (12.217), (12.218), and (12.189), respectively.
are defined in Equations (12.211), (12.212), (12.217), (12.218), and (12.189), respectively.



Next: Another Useful Lemma
Up: Terrestrial Ocean Tides
Previous: Useful Lemma
Richard Fitzpatrick
2016-03-31
![$\displaystyle = \frac{1}{\sin\theta}\left[\frac{\partial}{\partial\theta}\,(\sin\theta\,\eta) -\frac{\partial\xi}{\partial \phi}\right],$](img4762.png)
![$\displaystyle = \frac{1}{\sin\theta}\left[\frac{\partial}{\partial\theta}\,(\sin\theta\,\eta) -\frac{\partial\xi}{\partial \phi}\right],$](img4762.png)
![]() ,
,
![]() ,
,
![]() , and
, and
![]() in Equations (12.191)-(12.196). It
follows that
in Equations (12.191)-(12.196). It
follows that
![$\displaystyle =-\frac{1}{\sin\theta}\left[\frac{\partial}{\partial\theta}\,(\si...
...eta\,\cos\theta\,\eta)-\frac{\partial}{\partial\phi}\,(\cos\theta\,\xi)\right],$](img4770.png)
![$\displaystyle = -\frac{1}{\sin\theta}\left[\frac{\partial}{\partial\theta}\,(\s...
...a\,\cos\theta\,\xi) +\frac{\partial}{\partial \phi}\,(\cos\theta\,\eta)\right],$](img4772.png)